Теория систем автоматического управленияРасчет установившихся ошибок в автоматических системах
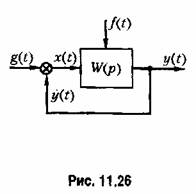
 приложенной в произвольной точке системы (рис. 11.26). приложенной в произвольной точке системы (рис. 11.26).
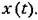 Обычно ограничиваются более узкой задачей и определяют только сред- Обычно ограничиваются более узкой задачей и определяют только сред-
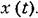
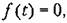 расчет можно свести к рассмотренной выше схеме (рис. 11.25). Тогда спектральная плотность ошибки будет расчет можно свести к рассмотренной выше схеме (рис. 11.25). Тогда спектральная плотность ошибки будет
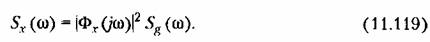
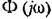 системы соотношением системы соотношением
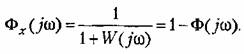
Таким образом, для спектральной плотности ошибки получаем

Интегрирование этого выражения по всем частотам позволяет определить дисперсию и среднеквадратичное значение ошибки:
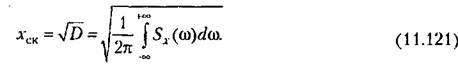
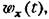 связанная с частотной передаточной функцией по ошибке преобразованием Фурье связанная с частотной передаточной функцией по ошибке преобразованием Фурье
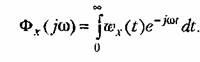
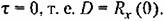
Однако нахождение среднеквадратичной ошибки посредством использования спектральных плотностей оказывается обычно более простым и поэтому применяется чаще.
 аналогичным образом можно найти спектральную плотность ошибки: аналогичным образом можно найти спектральную плотность ошибки:

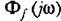 представляет собой час тотную передаточную функцию: представляет собой час тотную передаточную функцию:
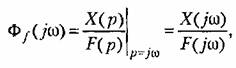
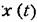 и по- и по-
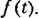
 действует на входе системы в месте приложения задающего воздействие действует на входе системы в месте приложения задающего воздействие
в формуле (11.101) должна использоваться частотная передаточная функция замкнутой системы:

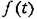 одновременно (рис. 11.26). одновременно (рис. 11.26).
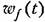 весовую функцию для ошибки но помехе. Тогда ошибку можно представить в виде весовую функцию для ошибки но помехе. Тогда ошибку можно представить в виде

Подставим это выражение для ошибки в формулу корреляционной функции (11.51). В результате получим
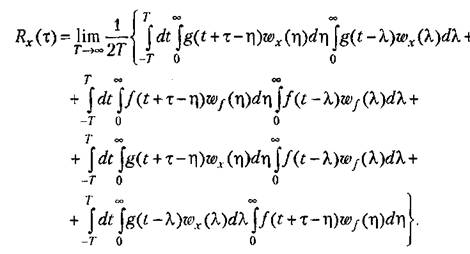
Отсюда находим
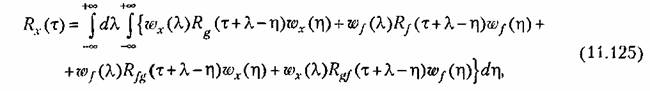
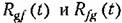 — взаимные корреляционные функции. — взаимные корреляционные функции.
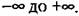 результате выкладок, аналогичных тем, которые были проделаны при выводе формулы (11.111), получим результате выкладок, аналогичных тем, которые были проделаны при выводе формулы (11.111), получим
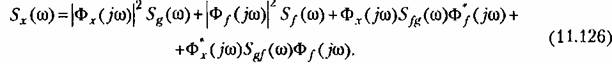
 частотные передаточные частотные передаточные
функции для ошибки по задающему воздействию и помехе. Звездочкой обозначен сопряженный комплекс,
При отсутствии корреляции между полезным сигналом и помехой формула (11.126) упрощается:
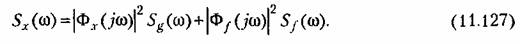
В частном случае, когда помеха действует на входе в месте приложения задающего воздействия и корреляция между ними отсутствует, формула (11.127) может быть представлена в следующем виде:

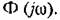
|