Теория систем автоматического управленияМетод стандартных переходных характеристик
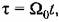 где где
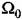 — среднегеометрический корень характеристического уравнения, определяющий быстродействие системы. — среднегеометрический корень характеристического уравнения, определяющий быстродействие системы.
При построении стандартных переходных характеристик необходимо задаться определенным распределением корней характеристического уравнения.
Ниже приводятся стандартные характеристики и соответствующие передаточные функции [44].
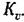
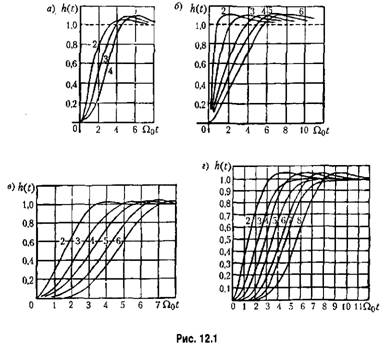
Нормированные переходные характеристики для каждого случая приведены па, рис. 12.1, а.
Для систем с астатизмом второго порядка корни также приняты вещественными, причем они составляют геометрическую прогрессию. Соответствующие передаточные функции приведены в табл. 12.2, а переходные характеристики — на рис. 12.1, б.

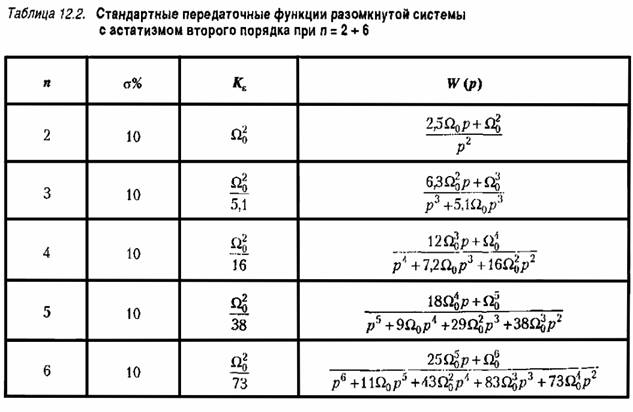
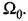 Далее оказываются известными все коэффициенты желаемой передаточной функции системы. Введением различных корректирующих средств необходимо добиться того, чтобы коэффициенты реальной передаточной функции были возможно ближе к коэффициентам желаемой передаточной функции. Далее оказываются известными все коэффициенты желаемой передаточной функции системы. Введением различных корректирующих средств необходимо добиться того, чтобы коэффициенты реальной передаточной функции были возможно ближе к коэффициентам желаемой передаточной функции.
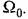 Далее расчет ведется так, как описано выше. Далее расчет ведется так, как описано выше.
Недостатком рассмотренного метода является то, что при построении стандартных переходных процессов приняты вещественные корни. Это во многих случаях не приводит к оптимальному решению. Однако стандартные переходные характеристики можно сравнительно просто построить для любого другого расположения корней, в том числе н для комплексных корней. Предлагается, например, такое решение [44]. Пусть характеристическое уравнение записано в виде
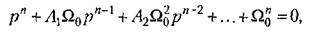
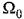 — среднегеометрический корень. — среднегеометрический корень.
Если принять все корни равными и вещественными, то это характеристическое уравнение приобретает вид

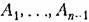 являются коэффициентами бинома Ньютона. являются коэффициентами бинома Ньютона.
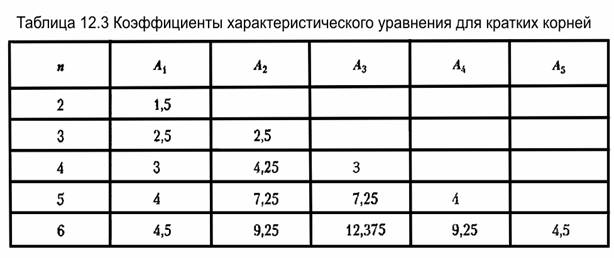
Однако переходный процесс затухает быстрее, если характеристическое уравнение при четном п имеет вид
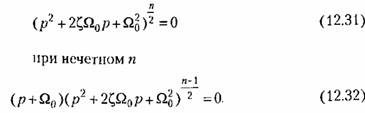
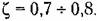
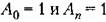 , для степени характеристического уравнения от 2 до 5. , для степени характеристического уравнения от 2 до 5.
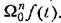
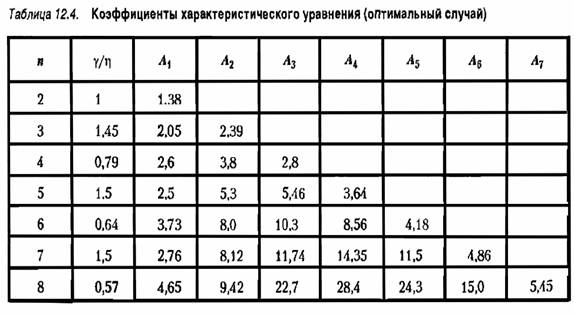
Переходный процесс затухает еще быстрее, если принять некратное распределение комплексных корней [44]. В этом случае все корни имеют одинаковую вещественную часть г]. Мнимые части корней образуют арифметическую прогрессию с разностью у и первым членом также у. Для каждой степени характеристического уравнения существует некоторое оптимальное отношение у/т], которому соответствует наибольшее быстродействие в безразмерном времени. Безразмерные коэффициенты характеристического уравнения для этого случая приведены в табл. 12.4, а переходные характеристики изображены па рис. 12.1, г.
При наличии нулей у передаточной функции принятые в табл. 12.3 и 12.4 распределения корней оказываются неудачными вследствие появления большого перерегулирования. В этом случае оказывается более выгодным использование расположения корней на вещественной оси по арифметической прогрессии (см. табл. 12.1 и 12.2).
|