Теория систем автоматического управленияСинтез систем автоматического управления на основе частотных критериев качества
Синтез систем автоматического управления методом логарифмических амплитудных характеристик является в настоящее время одним из самых удобных и наглядных. Наиболее трудным моментом при расчете методом логарифмических амплитудных характеристик является установление связи показателей качества переходного процесса с параметрами желаемой л. а. х„ что объясняется сравнительно сложной зависимостью между переходной характеристикой линейной системы и ее частотными свойствами. Задача построения желаемой л. а. х. значительно облегчается, если вместо оценки качества работы системы по ее переходной характеристике перейти к оценке качества непосредственно по ее частотным свойствам.
Для оценки качества любой системы управления, в том числе и следящей системы, необходимо знать ее точность, характеризуемую ошибками в некоторых типовых режимах, быстродействие, определяемое по способности системы работать при больших скоростях и ускорениях входного воздействия или по быстроте протекания пере- ходных процессов, и запас устойчивости, показывающий склонность системы к колебаниям. В соответствии с этим можно говорить о критериях точности, критериях быстродействия и критериях запаса устойчивости. При использовании частотных критериев необходимо основываться на тех или иных частотных свойствах системы.
При оценке точности по ошибкам при воспроизведении гармонического входного воздействия одновременно можно оценить и быстродействие по частоте этого воздействия. Тогда критерий точности и критерий быстродействия сливаются в один критерий динамической точности системы управления.
Ниже будут рассмотрены методы расчета систем, основанные на использовании частотных критериев качества. При этом кривая переходного процесса может, вообще говоря, не рассматриваться и не использоваться. Однако в целях иллюстрации будут даны универсальные нормированные кривые переходных процессов при единичном входном воздействии для рассматриваемых типовых л. а. х.
В дальнейшем изложении будут, как и ранее, рассматриваться линейные системы, состоящие из минимально-фазовых звеньев.
Под ошибкой следящей системы будет пониматься не действительное рассогласование между задающей и исполнительной осями, а только сигнал рассогласования, выявляемый чувствительным элементом системы. Это вызвано тем обстоятельством, что собственные ошибки чувствительных элементов, несмотря на их большой Удельный вес в полной ошибке системы управления, не оказывают влияния на статический и динамический расчет последней и должны учитываться отдельно. Вопросы расчета ошибок чувствительных элементов относятся к сфере теории соответствующих устройств (сельсинов, вращающихся трансформаторов, потенциометров и т. п.).
Методика расчета излагается в основном применительно к следящим системам воспроизведения угла и воспроизведения скорости. Однако эта методика применима и для других систем автоматического управления.
Требования к низкочастотной части желаемой л. а. х связанные с необходимой точностью. На основании требования поточности формируется низкочастотная часть желаемой л. а. х. следящей системы. Рассмотрим вначале астатические системы.
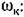

Амплитуда ошибки может быть найдена с помощью модуля передаточной функции по ошибке:
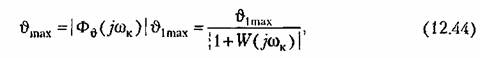
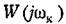 — частотная передаточная функция разомкнутой системы. — частотная передаточная функция разомкнутой системы.
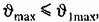 то справедливо соотношение то справедливо соотношение
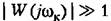 . Поэтому вместо (12.44) можно пользоваться приближенным выражением . Поэтому вместо (12.44) можно пользоваться приближенным выражением

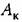 с координатами с координатами
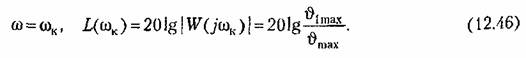
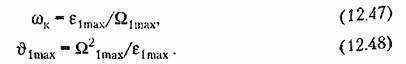
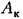 (рис. 12.8) в соответствии с (12.46). (рис. 12.8) в соответствии с (12.46).
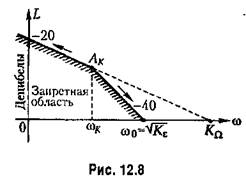
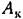 будет перемещаться влево по прямой, имеющей наклон -20 дБ/дек. В предельном случае, если принять амплитуду ускорения равной нулю, будет перемещаться влево по прямой, имеющей наклон -20 дБ/дек. В предельном случае, если принять амплитуду ускорения равной нулю,
 в известное соотношение в известное соотношение
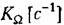 — предельное значение добротности по скорости следящей системы с — предельное значение добротности по скорости следящей системы с
астатизмом первого порядка, ниже которого нельзя иметь реальную добротность по скорости, исходя из условий точности.

равной отношению ускорения к установившейся ошибке. Это будет при условии, что первая асимптота л. а. х. проектируемой следящей системы совпадает с прямой, по которой движется контрольная точка Ак (рис. 12.8). Ниже этого предельного значения не может быть реальной добротности следящей системы с астатизмом второго порядка.
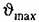 , если л. а. х. будет проходить не ниже запретной области. , если л. а. х. будет проходить не ниже запретной области.
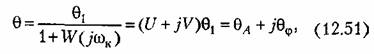 диаграмму, из которой следует диаграмму, из которой следует
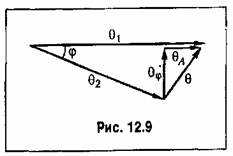
где II и V вещественная и мнимая части частотной передаточной функции по ошибке. Фазовая ошибка следящей системы

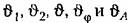
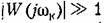 и передаточная функция разомкнутой системы с астатизмом первого порядка в области низких частот имеет вид и передаточная функция разомкнутой системы с астатизмом первого порядка в области низких частот имеет вид

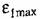
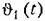 . При действии па систему возмущений, например момента нагрузки на оси двигателя, необходимо увеличение коэффициента передачи разомкнутой системы для того, чтобы результирующая ошибка не превосходила заданного значения. Более подробно это изложено, например, в [9]. . При действии па систему возмущений, например момента нагрузки на оси двигателя, необходимо увеличение коэффициента передачи разомкнутой системы для того, чтобы результирующая ошибка не превосходила заданного значения. Более подробно это изложено, например, в [9].
В статических системах установившаяся ошибка по задающему воздействию может быть сделана равной пулю применением неединичной обратной связи (§ 9.3), Однако появление статической ошибки возможно при нестабильности коэффициента передачи разомкнутой системы; В соответствии с формулой (9.66) для рассматриваемого случая максимальное значение ошибки составит

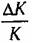 - относительное изменение коэффициента передачи разомкнутой системы. - относительное изменение коэффициента передачи разомкнутой системы.
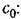

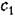 , являющегося коэффициентом пропорциональности между скоростью входного воздействия и ошибкой. , являющегося коэффициентом пропорциональности между скоростью входного воздействия и ошибкой.
Примем, что в низкочастотной области частотная передаточная функция статической системы может быть сведена к выражению

Формулы (12.57) и (12.59) устанавливают требования к низкочастотной части желаемой л. а. х.
Если к проектируемой системе кроме задающего воздействия приложено возмущение, то в формуле для коэффициента передачи разомкнутой системы необходимо дополнительно учесть составляющую, определяемую этим возмущением. Пусть, например, статическая ошибка от возмущения определяется формулой (8.4):
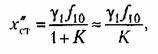
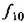 — постоянное возмущение. — постоянное возмущение.
Тогда вместо (12.56) можно записать
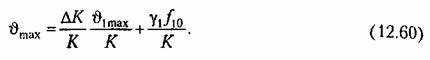
Отсюда находим требуемое значение коэффициента передачи:

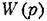 статической или астатической. статической или астатической.
Это значение коэффициента передачи будет определяться вторым слагаемым в правой части (12.61) или суммой подобных слагаемых при действии нескольких возмущений. По коэффициенту передачи может быть построена первая асимптота желаемой л. а. х.
|