Теория систем автоматического управленияПереходные процессы, соответствующие типовым Л. А. Х.
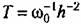
Чем больше протяженность участка А, тем меньше показатель колебательности и тем более благоприятным будет протекание переходного процесса, так как постоянная времени экспоненты будет меньше.
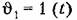 для случая использования л. а. х. типа 2-1-2 (рис. 12.10). для случая использования л. а. х. типа 2-1-2 (рис. 12.10).
Для нормированной передаточной функции (12.64) изображение Лапласа выходной величины будет иметь вид
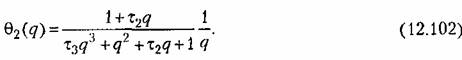
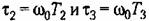 и затем построитьпереходный и затем построитьпереходный
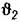 в функции безразмерного времени щс. Переходные характеристики показаны на рис. 12.19. в функции безразмерного времени щс. Переходные характеристики показаны на рис. 12.19.
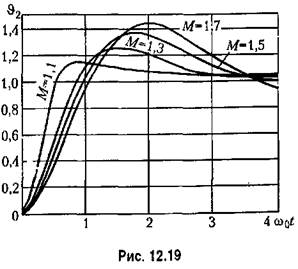
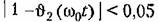 приведены в табл. 12.7. приведены в табл. 12.7.
Хотя эти кривые переходных процессов соответствуют л. а. х. типа 2-1-2 системы с астатизмом второго порядка (рис. 12.10), они с большой степенью точности могут использоваться для оценки переходных процессов при использовании л. а. х. других типов, изображенных, например, па рис. 12.13, 12.16 и 12.18, для которых характерным является наличие участка с наклоном -20 дБ/дек в районе пересечения оси частот.
Различие будет наблюдаться в начальной части, если высокочастотная часть л. а. х. отличается от высокочастотной части л. а. х. типа 2-1-2, и в конечной части, если будут отличаться их низкочастотные части. .
Таким образом, в случае нужды оценка переходных процессов может делаться по универсальным кривым, приведенным на рис. 12.19, во всяком случае для средней части кривой переходного процесса, которая показывает степень склонности системы к колебаниям.
В тех случаях, когда л. а. х. ие имеет специального участка с наклоном -20 дБ/дек при переходе оси частот (см. например, рис. 12.15 и 12.17), оценка переходных процессов может быть сделана следующим образом.
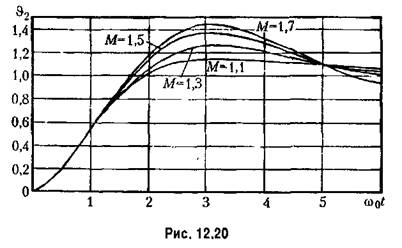
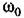 принята частота пересечения асимптоты, имеющей наклон -20 дБ/дек, с осью частот (рис. 12.15). Эти же кривые переходного процесса могут использоваться для оценки переходного процесса в случае использования л. а. х. другого тина, например 1-2-3 или 0-1-2 (рис. 12.17). Как и в предыдущем случае, различие может наблюдаться только в начальной и конечной стадиях переходного процесса. принята частота пересечения асимптоты, имеющей наклон -20 дБ/дек, с осью частот (рис. 12.15). Эти же кривые переходного процесса могут использоваться для оценки переходного процесса в случае использования л. а. х. другого тина, например 1-2-3 или 0-1-2 (рис. 12.17). Как и в предыдущем случае, различие может наблюдаться только в начальной и конечной стадиях переходного процесса.
Построение низкочастотной области желаемой л. а. х. Построение желаемой л. а. х. начинается с низкочастотной области. Из условий требуемой точности работы определяется положение контрольной точки или запретной области (см. рис. 12.8). Низкочастотная часть л. а. х. должна проходить не ниже контрольной точки или так, чтобы не заходить в запретную область.
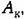 или сольется с правой границей запретной области (рис. 12.21). или сольется с правой границей запретной области (рис. 12.21).
 и необходимый коэффициент передачи разомкнутой и необходимый коэффициент передачи разомкнутой

системы определяются из выражения (12.50):

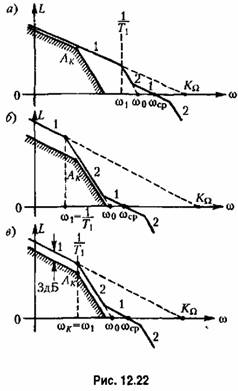
Если принять, что первая сопрягающая частота больше контрольной частоты не менее чем в 2-3 раза, то первые две асимптоты можно расположить так, чтобы через контрольную точку Лк прошла первая асимптота (рис. 12.22, а).
При этом коэффициент усиления по разомкнутой цепи пли добротность по скорости
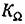 будет иметь минимальную возможную величину, равную предельному значению, определяемому из (12.49): будет иметь минимальную возможную величину, равную предельному значению, определяемому из (12.49):

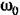 будет значительно больше минимального достижимого значения, определяемого по требуемому предельному коэффициенту передачи по ускорению (12.50). Это является нежелательным, так как вся л. а. х. будет сдвигаться в область более высоких частот, что будет значительно больше минимального достижимого значения, определяемого по требуемому предельному коэффициенту передачи по ускорению (12.50). Это является нежелательным, так как вся л. а. х. будет сдвигаться в область более высоких частот, что
затрудняет демпфирование вследствие относительного возрастания влияния всех постоянных времени системы.
 будет в 2-3 раза превышать минимальное возможное значение, определяемое формулой (12.50). Увеличение коэффициента передачи может неблагоприятным образом сказаться на возрастании влияния помех и наводок на входе. Поэтому выбор того или иного расположения низкочастотной части л. а. х. относительно контрольной точки должен определяться конкретными условиями. будет в 2-3 раза превышать минимальное возможное значение, определяемое формулой (12.50). Увеличение коэффициента передачи может неблагоприятным образом сказаться на возрастании влияния помех и наводок на входе. Поэтому выбор того или иного расположения низкочастотной части л. а. х. относительно контрольной точки должен определяться конкретными условиями.
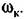
 должна быть поднята вверх на 3 дБ. При этом требуемое значение коэффициента передачи должна быть поднята вверх на 3 дБ. При этом требуемое значение коэффициента передачи

Точке пересечения второй асимптоты с осью нуля децибел соответствует частота

В статических следящих системах, а также в системах стабилизации построение низкочастотной части делается в соответствии с формулами (12.56)—(12.61).
Построение средне- и высокочастотной частей л. а. х. В системах с астатизмом второго порядка (рис. 12.21) необходимо осуществить типовой переход оси нуля децибел в соответствии с рис. 12.10. При этом известно значение базовой частоты Ц).
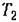 определяется формулой (12.73). определяется формулой (12.73).
Среднечастотпой части л. а. х. соответствует асимптота с единичным наклоном, проходящая в интервале амплитуд

Часть л. а. х., лежащая правее частоты среза, может иметь, вообще говоря, произвольный вид, определяемый имеющимися в системе звеньями. Однако в соответствии с изложенным выше необходимо выполнение следующих условий.
1. Высокочастотная часть л. а. х. не должна заходить в запретную область, образованную асимптотой с единичным наклоном, пересекающей ось пуля децибел в точке
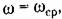 и горизонтальной прямой, соответствующей и горизонтальной прямой, соответствующей
 ) )
2. Сумма постоянных времени и коэффициентов при операторе в первой степени передаточных функций колебательных звеньев не должна превышать значения (12.82):
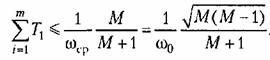
При построении желаемой л. а. х. в высокочастотной области вначале можно ориентироваться на наиболее простой ее вид и сформулировать ее при помощи одной асимптоты с наклоном -40 дБ/дек, положение которой определяется постоянной времени
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение

Эта л. а. х. показана в высокочастотной части на рис. 12.21 пунктирной линией. Она соответствует типу 2-1-2. При дальнейшем расчете вид высокочастотной части л. а. х. может уточняться. Однако два сформулированных выше условия не должны нарушаться. В окончательном виде высокочастотная часть л. а. х. может иметь произвольный вид, например показанный сплошной линией на рис. 12.21.
В следящих системах с астатизмом первого порядка необходимо вначале проверить возможность сведения желаемой л. а. х. к типу 1-2 или ее модификациям 1-2-3... Для этого необходимо исследовать возможность доведения суммы всех постоянных времени до значения, определяемого формулой (12.92):
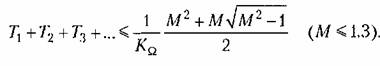
При отрицательном ответе необходимо сформировать переход оси нуля децибел асимптотой с единичным наклоном так, как показано па рис. 12.22. Весь расчет ведется аналогично изложенному выше для следящих систем с астатизмом второго порядка.
 — известны по построению низкочастотной части л. а. х. (см. рис. 12.22). — известны по построению низкочастотной части л. а. х. (см. рис. 12.22).
Для статических систем расчет ведется аналогично расчету систем с астатизмом первого порядка. Вначале необходимо проверить возможность использования л. а. х. типа 0-1-2 (рис. 12.17) или ее модификации 0-1-2-3... по формуле (12.100). При отрицательном ответе, необходимо сформировать переход оси нуля децибел аналогично рис. 12.21 и 19.22.
Расчет корректирующих (демпфирующих) средств
По наиболее простой схеме расчета корректирующие средства определяются сравнением желаемой передаточной функции с передаточной функцией системы без корректирующих средств или сравнением л. а. х., соответствующих этим передаточным функциям.
Часто эта схема расчета оказывается слишком упрощенной, что затрудняет ее использование. Это объясняется главным образом трудностью непосредственного перехода в сложных случаях от имеющейся передаточной функции к желаемой, а также тем обстоятельством, что формирование высокочастотной части л, а. х. может быть выполнено многозначно. Если вид желаемой л. а. х. в низкочастотной части является вполне определенным, то для ее высокочастотной части могут быть сформулированы лишь общие требования в отношении допустимой суммы постоянных времени и отсутствия пиков, заходящих в запретную зону (см. рис. 12.21).
Поэтому более гибкой оказывается схема расчета, при которой построение желаемой л. а. х. и расчет корректирующих средств, обеспечивающих получение желаемой л. а. х., делаются в два этапа.
На первом этапе расчета на основании требований к точности строится желаемая л. а. х. и рассчитываются корректирующие средства, формирующие ее в низкочастотной части. При этом будет получена некоторая промежуточная система, имеющая требуемую точность, но не имеющая, возможно, требуемого запаса устойчивости.
В некоторых случаях возможно сформирование одновременно с низкочастотной частью л. а. х. ее средне-, а в простейших случаях и высокочастотной частей.
На втором этапе расчета уточняется вид и рассчитываются параметры корректирующих средств, формирующих средне- и высокочастотную части л. а. х. В результате должна быть получена система, обеспечивающая не только требуемую точность в типовых режимах, но и имеющая необходимый запас устойчивости. Методы решения задачи оптимального синтеза будут рассмотрены в гл. 23.
|