Теория систем автоматического управленияСистемы с переменными параметрами
Основные понятия
Системами с переменными параметрами называются системы, движение которых описывается линейными дифференциальными уравнениями с переменными во времени коэффициентами:


 являются функциями времени, которые задаются либо графиками, построенными на основании эксперимента, либо аналитически. являются функциями времени, которые задаются либо графиками, построенными на основании эксперимента, либо аналитически.
Переменные коэффициенты в уравнении системы автоматического управления (13.1) возникают вследствие наличия переменных коэффициентов хотя бы в одном звене системы.
Так, например, у подвижного объекта (корабля, самолета, ракеты) с течением времени вследствие выгорания топлива происходит изменение массы и моментов инерции. Если объект при своем движении меняет скорость и высоту, то возможно изменение его аэродинамических коэффициентов.
В отличие от линейных систем с постоянными параметрами, методы анализа и синтеза которых были рассмотрены в предыдущих главах, исследование линейных систем с переменными параметрами представляет собой очень сложную задачу. В первую очередь это связано с тем, что в общем случае найти решение уравнения (13.1) невозможно. В результате, как правило, неприменимы разработанные для линейных систем с постоянными параметрами критерии устойчивости, оценки качества установившихся и переходных процессов, методы синтеза и др., а существующие специфические методы анализа и синтеза систем с переменными параметрами во многих случаях оказываются сложными для практического применения.
В связи с этим в данной главе рассматриваются лишь особенности систем с переменными параметрами и намечаются некоторые методы их исследования. Более подробно такие системы исследуются в работах [25, 86, 89] и др.
Рассмотрим переходную функцию и функцию веса системы с переменными параметрами. Так как коэффициенты уравнения (13.1) меняются с течением времени, то зти функции будут зависеть от момента приложения единичного скачка или единичного импульса на входе. На рис. 13.1, а изображен график изменения одного из коэффициентов уравнения (13.1) и переходная функция

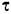 — текущее время, отсчитываемое от момента приложения ступенчатой функции. — текущее время, отсчитываемое от момента приложения ступенчатой функции.
Если теперь на вход подать единичную импульсную функцию, которую можно Представить как предел отношения
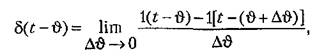
 раз масштабом: раз масштабом:
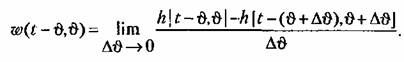
Правая часть этого выражения представляет собой производную от переходной функции по аргументу в, взятую с обратным знаком. Таким образом, для функции веса получаем (рис. 13.1, б)

 функция веса должна быть тождественно равна нулю. функция веса должна быть тождественно равна нулю.
 . Эта функция называется нормальной весовой функцией системы с переменными параметрами: . Эта функция называется нормальной весовой функцией системы с переменными параметрами:


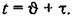 В результате получаем функцию В результате получаем функцию

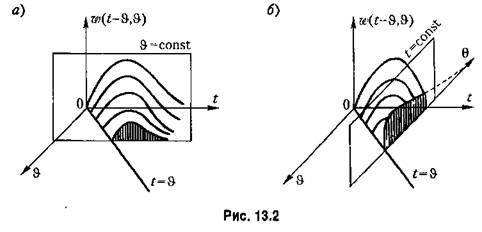
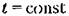 (рис. 13.2,6). (рис. 13.2,6).
 (рис. 13.3). Полу (рис. 13.3). Полу
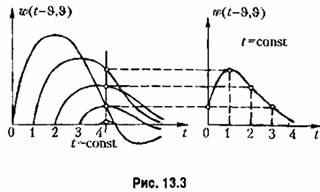
Получающуюся зависимость будем называть сопряженной функцией веса:

Она также является параметрической функцией, так как содержит параметр
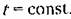
 В результате получаем В результате получаем

Проиллюстрируем все сказанное примером. Пусть функция веса системы с переменными параметрами имеет вид
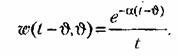
 получаем нормальную функцию веса: получаем нормальную функцию веса:



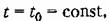 получаем со- получаем со-
пряженную функцию веса

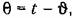 имеем имеем
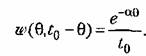
 и не зависит от момента приложения в входного и не зависит от момента приложения в входного

 действует входной сигнал действует входной сигнал
 будет будет



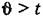 функция веса равна нулю, то выражение (13.9) можно также функция веса равна нулю, то выражение (13.9) можно также
записать в виде


 то интегральная связь (13.9) может быть представлена в виде интеграла свертки то интегральная связь (13.9) может быть представлена в виде интеграла свертки
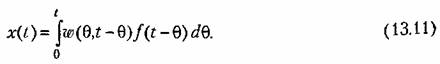
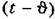 . В этом случае формула (13.11) переходит в интеграл свертки (7.44) . В этом случае формула (13.11) переходит в интеграл свертки (7.44)

|