Теория систем автоматического управленияНахождение функции веса и построение переходных процессов
Функция веса системы с переменными параметрами является исчерпывающей характеристикой этой системы, и нахождение ее важно но следующим соображениям. Функция веса характеризует протекание временных процессов в системе управления, и по ее виду можно судить о качестве управления, аналогично тому, как это делалось для систем с постоянным параметрами (§ 8.4). По имеющейся функции веса можно определить время протекания переходного процесса, как характеристику быстродействия и склонность системы к колебаниям.
Кроме того, по имеющейся функции веса можно строить процесс на выходе системы при заданных входных воздействиях не производя при этом каждый раз полного решения исходного уравнения (13.1). В соответствии с формулами (13.9) и (13.11) для этой цели необходимо иметь сопряженные функции веса.
Ввиду сложности проблемы существующие методы позволяют решать задачу нахождения функции веса в численном виде. Только для систем, описываемых дифференциальными уравнениями первого и иногда второго порядков, удастся решать задачу в общем виде. Поэтому в некоторых случаях приходится сложную систему с переменными параметрами приближенно сводить к более простой системе, движение которой описывается уравнением не выше второго порядка.
Следует заметить, что большинство систем управления с переменными параметрами относится к так называемым квазистационарным системам, и системам, параметры которых меняются сравнительно медленно. В подобных системах коэффициенты дифференциального уравнения (13.1) мало меняются в течение времени переходного процесса, определяемого временем затухания нормальной функции веса.
Дифференциальное уравнение первого порядка. В некоторых случаях для оценки вида переходных процессов системы с переменными параметрами ее уравнение приближенно можно свести к дифференциальному уравнению первого порядка

Это уравнение имеет аналитическое решение
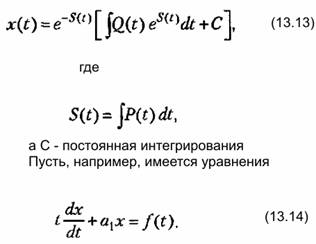
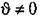 уравнение (13.14) можно записать в уравнение (13.14) можно записать в
следующем виде:
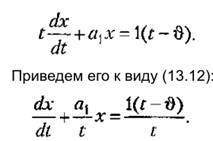
Далее получаем
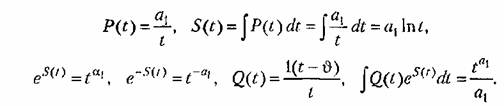
На основании формулы (13.13) получаем

При нулевых начальных условиях (для I = в) должно быть к (О, Ф) = 0. Отсюда определяется постоянная интегрирования
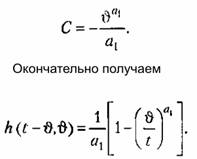
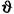 , можно получить функцию веса: , можно получить функцию веса:
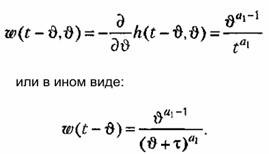
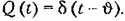 Проделав необходимые выкладки, получаем Проделав необходимые выкладки, получаем
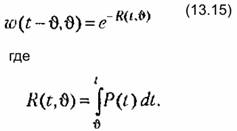
Распространим этот результат па более общий случай записи дифференциального уравнения в виде .

Рассмотрим снова в качестве примера уравнение (13.14). Приведем его к виду (13.17):
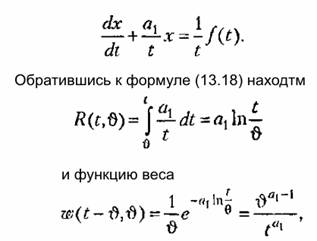
что совпадает с полученным ранее выражением.
Дифференциальное уравнение второго порядка. Рассмотрим случай, когда диф ференциальное уравнение (13.1) сводится к уравнению второго порядка

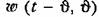
исходного уравнения (13.19) на основании формулы (13.20) соотношением
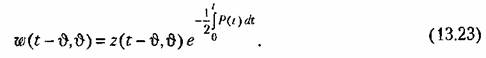
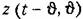 зависимостью зависимостью
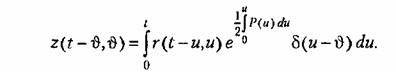
Эта зависимость на основании свойства дельта-функции может быть представ лена в виде
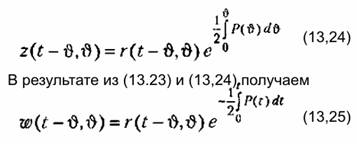
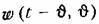 необходимо предварительно решить уравнение (13.21), которое приобретает вид необходимо предварительно решить уравнение (13.21), которое приобретает вид
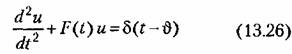
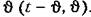
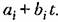 Однако это решение является сравнительно сложным. Однако это решение является сравнительно сложным.
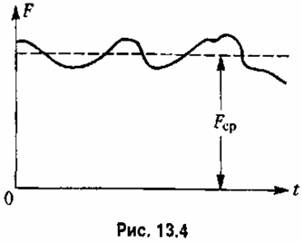
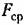 (рис, 13.4). Это решение называется аппроксимацией Бриллуина-Вентцеля-Крамера [86]. (рис, 13.4). Это решение называется аппроксимацией Бриллуина-Вентцеля-Крамера [86].
Рассмотрим однородное дифференциальное уравнение

Предположим теперь, что для некоторого однородного дифференциального уравнения второго порядка получено частное решение
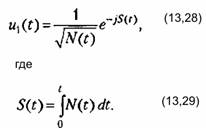
Найдем дифференциальное уравнение, которому удовлетворяет решение (13.28). Продифференцировав его дважды и исключив промежуточные переменные, получаем
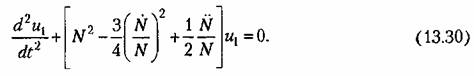
Сравнивая (13.30) и (13.27), видим, что выражение (13.28) будет частным решением уравнения (13.27), если выполняется тождество
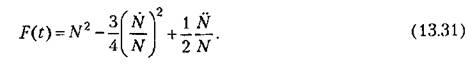
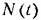 является сложной задачей вследствие наличия нелипейностей в (13.31). Однако может быть найдено приближенное решение (13.31) в виде ряда, если удовлетворяются неравенства является сложной задачей вследствие наличия нелипейностей в (13.31). Однако может быть найдено приближенное решение (13.31) в виде ряда, если удовлетворяются неравенства

Подставляя этот ряд в (13.31), получаем формулы для определения членов ряда:
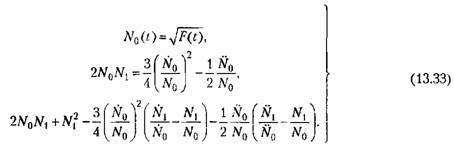
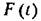 изменяется медленно, оставаясь в среднем большой (рис. 13.4). Тогда изменяется медленно, оставаясь в среднем большой (рис. 13.4). Тогда

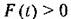 в качестве второго частного решения можно в качестве второго частного решения можно
взять комплексно-сопряженную величину (13.29)

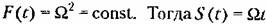
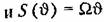 . В результате из формулы (13.37) можно получить функцию веса консервативного звена . В результате из формулы (13.37) можно получить функцию веса консервативного звена
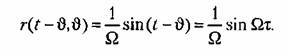
Для исходного дифференциального уравнения (13.19) на основании (13.25) и (13.37) получаем искомую функцию веса
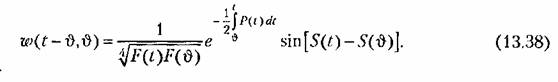
Критерием медленности изменения функции р {() и, следовательно, применимости полученного выражения может служить неравенство
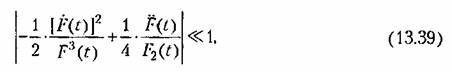
которое получается из (13.31) и (13.34).
|