Теория систем автоматического управленияО синтезе систем управления с ЦВМ
Синтез систем управления с ЦВМ наиболее просто производить па основе той методики, которая была изложена в § 12.6 для непрерывных систем. Покажем, как можно перенести ее на дискретные системы управления.
Как и в случае непрерывных систем, будем определять качество переходного процесса устойчивых дискретных систем, точнее их запас устойчивости, по показателю колебательности, соответствующему максимуму амплитудной частотной характеристики замкнутой системы:
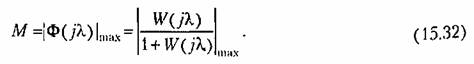
Соотношение (15.32) полностью аналогично соответствующему соотношению для непрерывных систем. Поэтому получение требуемого показателя колебательности может быть обеспечено выполнением условия для л. а. х. разомкнутой системы подобно тому, как это было сделано в § 12.6 для непрерывных систем.
Для упрощения выкладок ограничимся рассмотрением систем с астатизмом не выше второго порядка при наличии двух непрерывных интеграторов, хотя методика остается применимой и в случае более высокого порядка астатизма. Пустьиередаточ-ная функция непрерывной части разомкнутой системы имеет вид

При построении л. а. х. следящей системы с учетом ЦВМ введем следующие предположения.
 При расчете следящих систем с ЦВМ это неравенство приходится выполнять практически во всех случаях в связи с требованиями по устойчивости и запасу устойчивости. При расчете следящих систем с ЦВМ это неравенство приходится выполнять практически во всех случаях в связи с требованиями по устойчивости и запасу устойчивости.

 соответствуют сопрягающие частоты меньшие, чем частота среза. Это не относится к тем постоянным времени числителя передаточной функции разомкнутой непрерывной части, которые были введены для компенсации некоторых ее полюсов и поэтому после сокращения соответствующих множителей не вошли в окончательное выражение (15.33). соответствуют сопрягающие частоты меньшие, чем частота среза. Это не относится к тем постоянным времени числителя передаточной функции разомкнутой непрерывной части, которые были введены для компенсации некоторых ее полюсов и поэтому после сокращения соответствующих множителей не вошли в окончательное выражение (15.33).
Переход осп пуля децибел асимптотической л. а. х. непрерывной части происходит при отрицательном наклоне 20 дБ/дек.
Л. а. х. системы с ЦВМ в области низких частот. Рассмотрим построение л. а. х. для (15.33) в области низких частот, т. е. левее частоты среза. Передаточная функция непрерывной части для этой области может быть представлена в виде
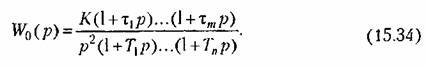
 Разложим (15.34) на простые дроби; Разложим (15.34) на простые дроби;
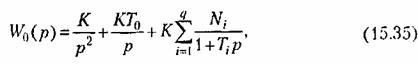
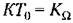 представляет собой условную добротность по скорости, а представляет собой условную добротность по скорости, а

На основании (14.60) дискретная передаточная функция, соответствующая (15.34),
будет

 преобразования (14.90) и подстановки (14.99). В результате получим преобразования (14.90) и подстановки (14.99). В результате получим
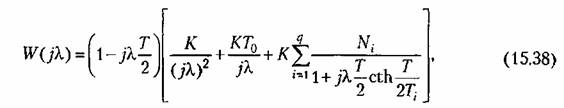
где абсолютная псевдочастота

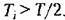 Поэтому можно считать Поэтому можно считать

Тогда окончательно
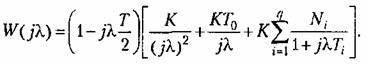
 Это дает большие удобства в формировании низкочастотной части л. а. х. проектируемой системы и позволяет полностью использовать ту методику, которая была изложена ранее для непрерывных систем. Это дает большие удобства в формировании низкочастотной части л. а. х. проектируемой системы и позволяет полностью использовать ту методику, которая была изложена ранее для непрерывных систем.
|