Теория систем автоматического управленияЛ. А. Х. Системы с цвм в области высоких частот
В соответствии с принятыми условиями передаточная функция непрерывной части для этой области может быть представлена в виде

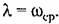
 , соответствующего неминимально-фазовому звену. /Для построения фазовой характеристики можно воспользоваться результирующим выражением для дискретной частотной передаточной функции, которое наосноваппм изложенного будет , соответствующего неминимально-фазовому звену. /Для построения фазовой характеристики можно воспользоваться результирующим выражением для дискретной частотной передаточной функции, которое наосноваппм изложенного будет
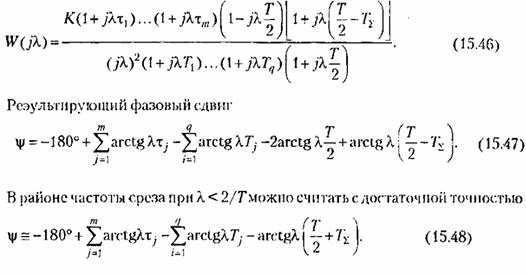
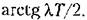 Методика расчета следящих систем с ЦВМ и здесь совпадает с методикой расчета непрерывных систем, изложенной выше. Только формула (12.83) должна быть переписана в виде Методика расчета следящих систем с ЦВМ и здесь совпадает с методикой расчета непрерывных систем, изложенной выше. Только формула (12.83) должна быть переписана в виде

Аналогичным образом для несимметричных л. а. х. типа 1-2-3 ... (рис. 12.15) систем с астатизмом первого порядка можно показать, что вид л. а. х. в низкочастотной области сохраняется, а требуемый запас устойчивости получится при
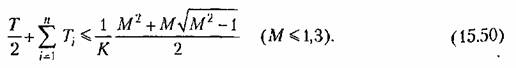
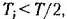 то для предотвращения захода высокочастотного хвоста л. а. х. в запретную зону (рис. 12.13) необходимо выполнить дополнительное условие то для предотвращения захода высокочастотного хвоста л. а. х. в запретную зону (рис. 12.13) необходимо выполнить дополнительное условие
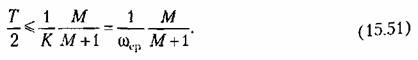
 а употреб-пять обычное обозначение со, считая, что в области рабочих частот (левее частоты среза) это есть частота входного воз действия, а в высокочастотной области она переходит в псев дочастоту. а употреб-пять обычное обозначение со, считая, что в области рабочих частот (левее частоты среза) это есть частота входного воз действия, а в высокочастотной области она переходит в псев дочастоту.
Сделаем теперь два замеча ния. Первое относится к случаю наличия в передаточной функ ции непрерывной части (15.33) сомножителей, соответствующих
колебательным звеньям с передаточной функцией

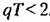 , то дискретная частотная передаточная функция , то дискретная частотная передаточная функция
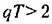 построение л. а. х. несколько усложняется вследствие явления транспонирования частот. Однако и здесь не возникает никаких принципиальных трудностей [9]. построение л. а. х. несколько усложняется вследствие явления транспонирования частот. Однако и здесь не возникает никаких принципиальных трудностей [9].
 не выполняется, то построение л. а. х. не выполняется, то построение л. а. х.

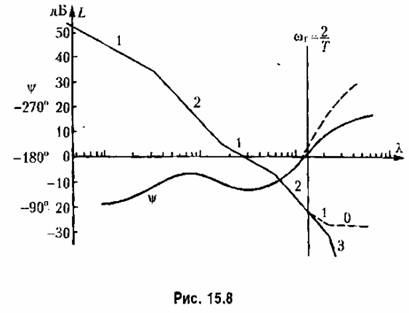
Далее находится формула, соответствующая высокочастотной части л. а. х. непрерывной системы, аналогичная формуле (15.41). Пусть, например, пересечение граничной частоты происходит при наклоне асимптоты -40 дБ/дек так, как это показано на рис. 15.8. Тогда уравнение высокочастотной части будет
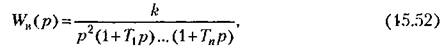
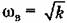 — частота пересечения оси частот асимптотой, имеющей отрицательный наклон 40 дБ/дек. — частота пересечения оси частот асимптотой, имеющей отрицательный наклон 40 дБ/дек.
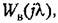 получим аналогично формуле (15.44) для высокочастотной части получим аналогично формуле (15.44) для высокочастотной части

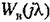 строится высокочастотная часть л. а. х., строится высокочастотная часть л. а. х.,
которая показана на рис. 15.8 пунктиром.
Построение фазовой характеристики делается аналогично изложенному выше.

II р и м е р. Произведем расчет следящей системы с астатизмом второго порядка при следующих исходных данных:
 = 10 град/с; = 10 град/с;
 - 5 град/с2; - 5 град/с2;
 = 2 угл. мин.; = 2 угл. мин.;
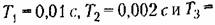 = 0,001 с; = 0,001 с;
5) допустимый показатель колебательности М= 1,5 и М- 1,2.
Требуется определить параметры непрерывной части системы и допустимый период дискретности Т.
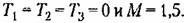 Передаточная функция Передаточная функция
непрерывной части разомкнутой системы, структурно устойчивой в замкнутом состоянии, должна иметь вид

 — постоянная времени, вносимая корректирующим звеном дифференцирующего тина. — постоянная времени, вносимая корректирующим звеном дифференцирующего тина.



Б соответствии с формулой (15.41) получаем далее

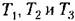 имеем имеем
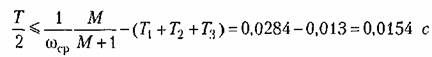
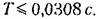
 с с
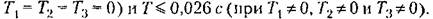
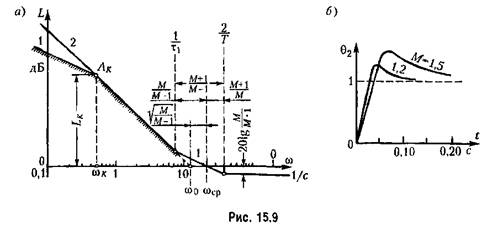
На рис. 15.9, б для иллюстрации построены переходные процессы при воздействии на входе в виде единичной ступенчатой функции. Переходные процессы построены посредством разложения вряд Лорана z-преобразования выходной величины.
Таким образом, синтез следящих систем методом л. а. х. на основе частотных критериев качества (но точности и запасу устойчивости) оказывается применимым и для систем, содержащих в своем контуре ЦВМ. При этом все расчеты сохраняют свою простоту и наглядность.
Для расчета удобно применять абсолютную псевдочастоту которая в области низких частот (левее частоты среза) совпадает с обычной угловой частотой со. При этом в области высоких частот л. а. х. приходится строить по сумме малых постоянных времени. Влияние квантования по времени, вносимое ЦВМ, легко учитывается при построении только л. а. х., без необходимости рассмотрения фазовой характеристики.
Для облегчения процесса синтеза можно ввести понятие типовых л. а. х. систем управления с ЦВМ. На рис. 15.10, я приведены типовые л. а. х. для статической системе и астатической первого и второго порядков без учета временного запаздывания. На рис. 15.10,6 изображены соответствующие им л. а. х. непрерывной части, а в табл. 15.2 приведены передаточные функции.
|