Теория систем автоматического управленияОсобые линии для нелинейных систем
Реальные системы автоматическою управления можно считать линейными чаще всего в предположении малости отклонений переменных от их значений в определенном установившемся состоянии.
За пределами указанной области вследствие значительного отклонения характеристик от линейных картина фазовых траекторий может сильно измениться и стать качественно иной.
В частности, если по линейной теории система оказывается неустойчивой и процесс начинает расходиться, то может оказаться, что из-за фактической нелинейности характеристик он не будет расходящимся неограниченно. Амплитуда расходящихся колебаний может увеличиваться только до определенного значения, а затем оставаться постоянной, т. е. неустойчивая линейная автоматическая система как бы превращается в устойчивую нелинейную автоколебательную систему (система генерирует устойчивые колебания определенной формы).
Картина фазовых траекторий для такой системы изображена на рис. 16.14, а. Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе (рис. 16.10, б), но далее все они расходятся не до бесконечности, а приближаются
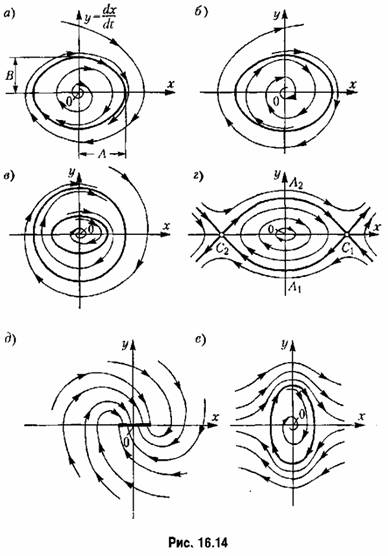
асимптотически к некоторому замкнутому контуру ограниченных размеров,как показано парне. 16.14, а. К нему же приближаются и все спирали, находящиеся вне контура. Это соответствует картине процессов во времени, изображенной па рис. 16.3, а. Такого вида замкнутый контур, представляющий собой наиболее важный для теории тип особыхлипнй на фазовой плоскости, называется устойчивым предельным циклом.
Устойчивый предельный цикл соответствует автоколебаниям системы. Размеры предельного цикла А и В (рис. 16.14, а) представляют амплитуды колебаний самой величины х и скорости ее их изменения у-— . для (к
определения периода автоколебаний надо обратиться к решению уравнений во времени.
Случаю устойчивости системы в малом и неустойчивости в большом (рис. 16.3, б) соответствует картина фазовых траекторий, изображенная на рис. 16.14, б. Граница начальных условий, до которой система устойчива, имеет чаще всего на фазовой плоскости вид неустойчивого предельного цикла, как на рис. 16.14, б, от которого в обе стороны удаляются спиралевидные фазовые траектории. Это — второй важный тип особых линий, определяющий устойчивость системы в малом и неустойчивость в большом.
Заметим, что в этом случае может быть также еще более удаленный устойчивый предельный цикл (рис. 16.14, о), соответствующий автоколебаниям с большой амплитудой. Это соответствует процессам во времени, изображенным на рис. 16.3, г. Таких же принципиальные качественные изменения картины фазовых траекторий при достаточно больших отклонениях могут наблюдаться и в случаях апериодических процессов (рис. 16.12, б и 16.13, б), включая превращения их в колебательные и наоборот. Например, картине процессов во времени, показанной на рис. 16.3, в, соответствует картина фазовых траекторий па рис. 16.14, е.
 что что
 (рис. 16.14,г), на фазовой плоскости называются сепаратрисами (третий тип особых липни). Особые линии более сложного очертания рассматриваться не будут. (рис. 16.14,г), на фазовой плоскости называются сепаратрисами (третий тип особых липни). Особые линии более сложного очертания рассматриваться не будут.
Здесь говорилось пока о системах, которые при малых отклонениях рассматриваются как линейные. Но совершенно аналогичная картина получается и для таких нелинейных систем автоматического управления, которые даже в малом*- нельзя рассматривать как линейные. Таковыми являются многочисленные типы релейных систем, а также системы с зоной нечувствительности, с гистерезмспой петлей, с сухим трением, с зазором. Интересно отметить, что некоторые из таких систем скорее в большом, чем в малом, могут приближаться к линейным, когда зона нечувствительности или зазор оказываются малыми по сравнению с величиной отклонений л:.
В системах с зоной нечувствительности и с сухим трением существуют, как известно, области застоя, когда установившемуся состоянию при данных внешних условиях (данной нагрузке) соответствует не одна точка, а целая область возможных равновесных состояний системы. На фазовой плоскости это выражается, в том, что особая точка вытягивается в особый отрезок (рис. 16.14, д).
Заметим, наконец, что координатами (х,у) фазовой плоскости могут служить не обязательно отклонения управляемой величины и скорость ее, как было выше. Для этой цели могут быть взяты любые две переменные, однозначно характеризующие состояние системы второго порядка в произвольный момент времени.
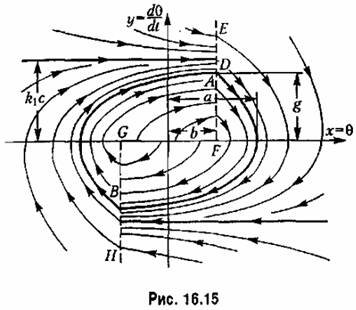
Пример. Изобразим па фазовой плоскости переходный процесс и автоколебания системе стабилизации температуры, рассмотренной выше. Координаты фазовой плоскости будут


(линия СН). Справа от липни переключения EFGH справедливо уравнение системы (16.12), а слева-(16.13).
Уравнение (16.12) в обозначениях (16.29) примет вид

откуда получаем дифференциальное уравнение фазовых траекторий

Интегрирование его дает

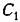 — произвольная постоянная. — произвольная постоянная.
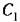 соответствует определенная кривая на соответствует определенная кривая на
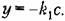 Направление движения изображающей точки по ним, показанное Направление движения изображающей точки по ним, показанное
стрелками, определяется из условия
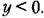
Уравнение (16.13) в обозначениях (16.29) будет
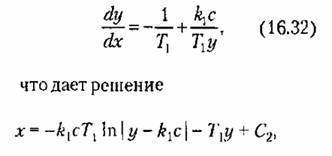
 (рис. 16.15). (рис. 16.15).
В результате получится, что фазовые траектории расходятся от начала координат и сходятся из бесконечности, т. е. имеет место случай, аналогичный рис. 16.14, а, а значит, где-то должен быть устойчивый предельный цикл. Он обозначен жирной линией на рис. 16.15.
Следовательно, в данной системе будут наблюдаться автоколебания, к которым сходится переходный процесс с обеих сторон, т. е. при любых начальных условиях.
 невозможно. Амплитуда автоколебаний температуры в данной системе изображается на рис. 16.15 отрезком a. Период же автоколебаний определяется решением уравнений во времени, как было сделано выше. Половины AB и ВD (рис. 16.15) предельного никла соответствуют полупериодам AВ и ВD (рис. 16.4, б) автоколебаний. невозможно. Амплитуда автоколебаний температуры в данной системе изображается на рис. 16.15 отрезком a. Период же автоколебаний определяется решением уравнений во времени, как было сделано выше. Половины AB и ВD (рис. 16.15) предельного никла соответствуют полупериодам AВ и ВD (рис. 16.4, б) автоколебаний.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение

Перейдем к составлению уравнений нелинейных систем автоматического управления,
|