Построение высоконадежных системПроведение проверок работоспособности

Представим, что устройство функционирует таким образом, что во время работы мы не можем, не нарушая нормального процесса его эксплуатации, удостовериться в том, исправно оно или нет. В то же время нахождение устройства в состоянии необнаруженного отказа — это его простой в самом обычном смысле слова.
Нам уже известно, что в подобных случаях проведение предупредительных профилактических замен не имеет смысла, так как по своим вероятностным характеристикам новое устройство ничем не лучше того, которое проработало уже в течение произвольного времени.
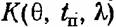 — коэффициент использования устройства — коэффициент использования устройства
(т. е. доля полезного рабочего времени) был максимальным.
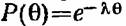 за время 0 отказ не произойдет, за время 0 отказ не произойдет,
 в таком интервале будет иметь плотность в таком интервале будет иметь плотность

 как нетрудно получить после простых преобразований, равно как нетрудно получить после простых преобразований, равно

 обеспечивающее максимум функции обеспечивающее максимум функции

Отыскивая экстремум обычным способом, получаем трансцендентное уравнение

 максимизирующее коэффициент использования устройства максимизирующее коэффициент использования устройства
 то можно записать с хорошей степенью приближения: то можно записать с хорошей степенью приближения:

Оптимизация процедур поиска неисправных элементов. С ростом сложности технических систем все острее встает проблема их ремонтоспособности и сокращения времени простоя в процессе эксплуатации. В этой связи одной из важных задач является задача организации оптимальных процедур поиска неисправных элементов.
Конечно, эта задача должна решаться и реально решается с учетом конкретных особенностей той или иной технической системы, ее структуры, конструктивного оформления, характера эксплуатации, степени обученности эксплуатирующего данную систему технического персонала и других факторов. Однако и в этом случае бывает важно иметь достаточно общие математические модели, описывающие процедуры поиска неисправных элементов в сложных системах, так как такие модели могут помочь сформулировать важные для практики инженерные рекомендации.
Рассмотрим следующую ситуацию [7]. На ремонтную базу поступило некоторое устройство, состоящее из п элементов. (Повторим, что под элементом может пониматься любая часть рассматриваемого устройства, разделять которую на составные части не имеет смысла в рамках данного исследования.) Требуется путем проведения проверок отдельных элементов выявить все неисправные элементы системы, заменив их в процессе проверки на исправные. При проверке допускаются тесты лишь двух видов: глобальный тест, на основании успешного проведения которого можно сделать заключение об исправности всего устройства в целом, и локальный тест каждого отдельного элемента, на основании которого можно сделать заключение об исправности лишь данного проверяемого элемента.
 найти порядок проведения проверок, отдельных элементов, обеспечивающий выявление всех имеющихся неисправностей при минимальных в среднем затратах. (Затраты в данном случае могут измеряться в различных единицах — человеко-часах, необходимых для проведения проверок, времени простоя, стоимостных единицах и т. п.) найти порядок проведения проверок, отдельных элементов, обеспечивающий выявление всех имеющихся неисправностей при минимальных в среднем затратах. (Затраты в данном случае могут измеряться в различных единицах — человеко-часах, необходимых для проведения проверок, времени простоя, стоимостных единицах и т. п.)
 соответствии с этими номерами поочередно проверяются. Как только обнаруживается неисправный элемент, он заменяется на исправный, и сразу же проводится глобальный тест, чтобы удостовериться в том, имеются ли в устройстве еще неисправные элементы. Если глобальный тест не проходит успешно, то продолжается поэлементная проверка. соответствии с этими номерами поочередно проверяются. Как только обнаруживается неисправный элемент, он заменяется на исправный, и сразу же проводится глобальный тест, чтобы удостовериться в том, имеются ли в устройстве еще неисправные элементы. Если глобальный тест не проходит успешно, то продолжается поэлементная проверка.
 является неисправным и поэтому проверка еще не закончилась . Вероятность этого события равна является неисправным и поэтому проверка еще не закончилась . Вероятность этого события равна

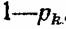
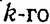 элемента. Вероятность этого события не нужна при дальнейших расчетах. элемента. Вероятность этого события не нужна при дальнейших расчетах.
 элемента, легко находятся как элемента, легко находятся как

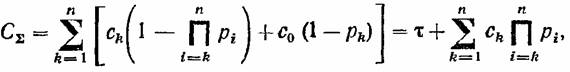 средние затраты по всем элементам: средние затраты по всем элементам:
 — затраты, не зависящие от нумерации элементов. Из полученного выражения видно, что средние затраты на проверку всего устройства зависят от того, в каком порядке мы будем проверять элементы. Это совершенно ясно, если взять "крайний случай: систему, состоящую из двух элементов — одного очень надежного, но требующего больших затрат на проверку, и второго малонадежного, требующего очень малых затрат на проверку. Проведение проверки, начиная со второго элемента, совершенно очевидно. — затраты, не зависящие от нумерации элементов. Из полученного выражения видно, что средние затраты на проверку всего устройства зависят от того, в каком порядке мы будем проверять элементы. Это совершенно ясно, если взять "крайний случай: систему, состоящую из двух элементов — одного очень надежного, но требующего больших затрат на проверку, и второго малонадежного, требующего очень малых затрат на проверку. Проведение проверки, начиная со второго элемента, совершенно очевидно.
Однако в более сложных ситуациях выбор порядка проверки элементов далеко не очевиден.
 , и посмотрим, при каких условиях , и посмотрим, при каких условиях
такая перемена приводит к сокращению средних суммарных затрат. Выражение средних суммарных затрат в этом случае будет равно:

Естественно, что подобная перестановка порядка проверки соседних элементов целесообразна, если выполняется условие

Проведя элементарные преобразования, находим, что условие (17) выполняется, если

Поскольку при конечном числе перестановок соседних элементов может быть получено любое наперед заданное их размещение, становится ясным, что при нумерации элементов в порядке возрастания величин

никакая перестановка не может привести к уменьшению средних суммарных затрат.
Интересно заметить, что затраты, связанные непосредственно с устранением отказа, никак не влияют на нумерацию элементов с точки зрения минимизации суммарных средних затрат. Это легко объяснить, исходя из того, что затраты на ремонт элемента не зависят от порядка проверки элемента.
В более сложных случаях, когда, например, проверки охватывают не один, а несколько элементов, решение задали существенно усложняется .
|