Теория систем автоматического управленияТеоремы прямого метода Ляпунова и их применение
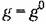 Следовательно, эти уравнения для нелинейной системы п-го порядка будут: Следовательно, эти уравнения для нелинейной системы п-го порядка будут:
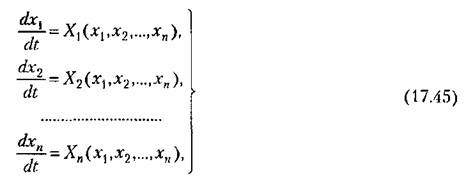
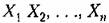 произвольны и содержат любого вида нелинейности, но произвольны и содержат любого вида нелинейности, но
всегда удовлетворяют условию
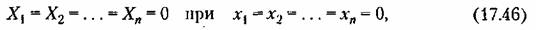
так как в установившемся состоянии все отклонения переменных и их производные равны, очевидно, нулю но самому определению понятия этих отклонений.
Нам понадобятся в дальнейшем еще следующие сведения.
Понятие о знакоопределенных, знакопостоянных и знакопеременных функциях. Пусть имеется функция нескольких переменных
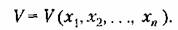
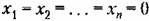 ) и непрерывны в некоторой области вокруг него. ) и непрерывны в некоторой области вокруг него.
Функция У называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат.
Функция Указывается знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.
Функция Указывается знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.
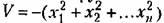 — знакоопределенной отрицательной. — знакоопределенной отрицательной.
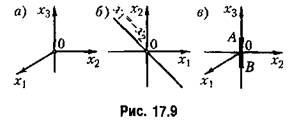
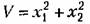 при п = З.то она уже не будет знакоопределепной, при п = З.то она уже не будет знакоопределепной,
 , рис. 17.9, а). Следовательно, это будет знакопостоянная (положительная) функция. , рис. 17.9, а). Следовательно, это будет знакопостоянная (положительная) функция.
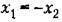 (рис. 17.9, б) и отрицательна слева от этой прямой. (рис. 17.9, б) и отрицательна слева от этой прямой.
Заметим, что в некоторых частных задачах нам понадобится также функция V, которая обращается в нуль не в начале координат, а на заданном конечном отрезке АВ (рис. 17.9, в). Тогда знакоопределенность функции V будет обозначать ее неизменный знак и необращение в нуль в некоторой области вокруг этого отрезка.
|