Теория систем автоматического управленияФункция Ляпунова и ее производная по времени
Любую функцию

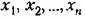 взяты те отклонения неременных в переходном процессе взяты те отклонения неременных в переходном процессе
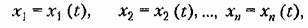
в которых записываются уравнения (17.45) для этой системы. Производная от функции Ляпунова (17.47) по времени будет
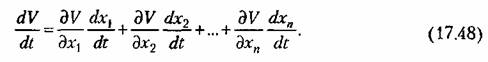
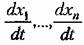 из заданных уравнений система в общем из заданных уравнений система в общем
случае (17.45), получим производную от функции Ляпунова по времени в виде
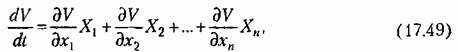
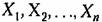 — правые части уравнений (17.45), представляющие собой заданные — правые части уравнений (17.45), представляющие собой заданные
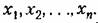
Следовательно, производная от функции Ляпунова по времени, так же как и сама V, является некоторой функцией отклонений, т. е.

 - Поэтому к ней в одинаковой степени можно - Поэтому к ней в одинаковой степени можно
применять веете же понятия знакоопределенности, знакопостояпства и знакопеременности в некоторой области вокруг начала координат, о которых говорилось выше по отношению к функции V.
Здесь шла речь только об уравнениях (нелинейных), в которые не входит в явном виде время t, так как только этот случай будет рассматриваться в дальнейшем. Вообще же метод Ляпунова может применяться и при наличии времени I в явном виде, в частности для уравнений с переменными коэффициентами (линейных и нелинейных).
Базируясь на этих предварительных сведениях, дадим общую формулировку теорем Ляпунова об устойчивости и неустойчивости нелинейных систем и покажем их справедливость. Теоремы эти годятся для исследования устойчивости систем управления не только при малых, но и при больших отклонениях, если для них справедливы исходные уравнения данной системы управления. Устойчивость системы при любых больших начальных отклонениях называется коротко — устойчивостью в целом.
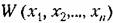 тоже была знакоопределенной (или знакопостоянной), по имела знак, противоположный знаку V, то данная система устойчива. При знакоопределенной функции W будет иметь место асимптотическая устойчивость, тоже была знакоопределенной (или знакопостоянной), по имела знак, противоположный знаку V, то данная система устойчива. При знакоопределенной функции W будет иметь место асимптотическая устойчивость,
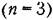 . Уравнения (17.45) . Уравнения (17.45)
для нее в общем виде будут
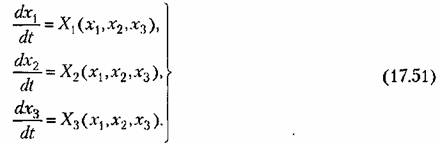
Возьмем зиакоопределенную положительную функцию Ляпунова в виде
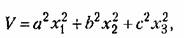 (17.52) (17.52)
где а,b,с — произвольно заданные вещественные числа.
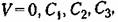 ..., что означает ..., что означает
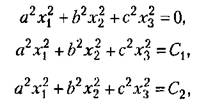
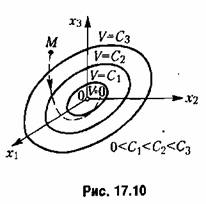
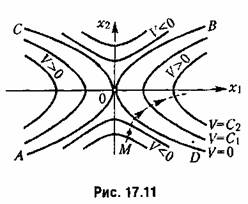
 (началу координат фазового пространства), а остальные -- поверхностям ;оллинсоидов в фазовом пространстве, причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий (рис. 17.10). (началу координат фазового пространства), а остальные -- поверхностям ;оллинсоидов в фазовом пространстве, причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий (рис. 17.10).
Возьмем теперь производную от функции Ляпунова но времени. Согласно (17.49) и (17.52)
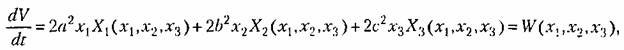
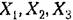 берутся из заданных уравнений системы (17.51). берутся из заданных уравнений системы (17.51).
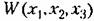 окажется знакоопределенной окажется знакоопределенной
отрицательной, т. е. если

во всех точках исследуемого фазового пространства, кроме одного только начала координат, где
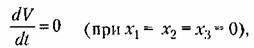
то при любых начальных условиях изображающая точка М (рис. 17.10) вследствие (17.53) будет двигаться в сторону уменьшения значения V, т. е. будет пересекать эллипсоиды, изображенные на рис. 17.10, извне внутрь. В результате с течением времени изображающая точка М будет стремиться к началу координат О фазового пространства (асимптотическая устойчивость) и уже никак не сможет выйти за пределы тех эллипсоидов, в которые она проникла.
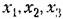 в переходном процессе с тече- в переходном процессе с тече-
нием времени. Таким образом, установлена устойчивость данной системы, что иллюстрирует справедливость теоремы для системы третьего порядка (в случае знакооире-деленной функции У/).
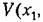
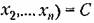 получим некоторые замкнутые поверхности, окружающие начало координат (рис. 17.10), но уже I не в обычном трехмерном, а в n-мерном фазовом пространстве (их иногда называют гиперповерхностями). получим некоторые замкнутые поверхности, окружающие начало координат (рис. 17.10), но уже I не в обычном трехмерном, а в n-мерном фазовом пространстве (их иногда называют гиперповерхностями).
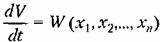 ока- ока-
жется зпакооиределепной отрицательной, то траектория изображающей точки М в n-мерном пространстве при любых начальных условиях с течением времени будет пересекать указанные поверхности только извне внутрь, что и свидетельствует об устойчивости данной системы.
Если же функция Избудет не зиакоопределенной, а знакопостоянной, то очевидно, что траектория изображающей точки М не везде будет пересекать поверхности V = С, а может их касаться в тех точках, где W обращается в нуль (помимо начала координат). Но так как во всех других местах фазового пространства функция W имеет один и тот же знак, вследствие чего изображающая точка может идти только извне внутрь поверхности V = С то при решении задачи остается только проверить, не застрянет ли изображающая точка там, где W = 0 (см. пример ниже).
Замечания к теореме Ляпунова об устойчивости. По поводу сформулированной теоремы Ляпунова об устойчивости системы необходимо сделать следующие два важных замечания.
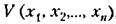 . Вообще говоря, при заданных в форме (17.45) уравнениях системы управления можно подо брать несколько различных вариантов функции V, поскольку требуется только знакоопределенность ее и ее производной. Различные варианты функции V, удовлетворяющие теореме, могут дать соответственно различные варианты условий устойчивости для одной и той же системы. При этом одни из них будут шире, другие уже, последние могут входить в первые как частный случай и т, д. . Вообще говоря, при заданных в форме (17.45) уравнениях системы управления можно подо брать несколько различных вариантов функции V, поскольку требуется только знакоопределенность ее и ее производной. Различные варианты функции V, удовлетворяющие теореме, могут дать соответственно различные варианты условий устойчивости для одной и той же системы. При этом одни из них будут шире, другие уже, последние могут входить в первые как частный случай и т, д.
Поэтому, вообще говоря, данная теорема Ляпунова обеспечивает получение достаточных условий устойчивости, которые не всегда будут и необходимыми, т. е, при выполнении условий теоремы система наверняка будет устойчивой, но эти условия могут не охватывать всей области устойчивости системы но параметрам. В самом деле, если выбрана функция V, удовлетворяющая теореме, пет уверенности в том, что нельзя подобрать другой вариант функции V, который бы еще более полно охватывал область устойчивости данной системы,
Геометрически это значит, что, получив определенное семейство поверхностей V = С (рис. 17.10) и убедившись, что траектории изображающей точки М приближаются к началу координат, пересекая эти поверхности извне внутрь, нельзя быть уверенным в том, что не существует еще других вариантов траекторий изображающей точки А/, которые в отдельных местах могут пересекать данные поверхности изнутри вовне, по все же с течением времени в конце концов неограниченно приближаться к началу координат. Такие траектории будут соответствовать другому семейству поверхностей V= С, т. е. другому варианту выбора функции Ляпунова.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
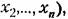 которые соответствуют всей области устойчивости. которые соответствуют всей области устойчивости.
 система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него. система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него.
Теорема Ляпунова о неустойчивости нелинейных систем. Поскольку предыдущая теорема Ляпунова дает, вообще говоря, только достаточные условия устойчивости и поскольку кроме области устойчивости нелинейная система может иметь целый ряд особых областей то может возникнуть потребность в отдельном определении области неустойчивости путем использования нижеследующей теоремы Ляпунова, которая дает достаточные условия неустойчивости системы.
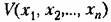 окажется знакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива. окажется знакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива.
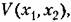 для которой производная для которой производная
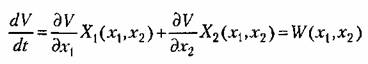
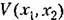 на фа- на фа-
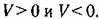
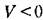 и везде и везде
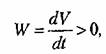
то изображающая точка М с течением времени будет двигаться и пересекать линии V = С, переходя от меньших значений С к большим. Она может при этом лишь временно приблизиться к началу координат, но в конце
концов будет неограниченно удаляться от начала координат. Это соответствует расходящемуся процессу, т. е. неустойчивости системы. Аналогично можно показать справедливость теоремы и для системы любого порядка п, проводя те же рассуждения для га-мерного фазового пространства.
Приведем два примера применения изложенных теорем Ляпунова к исследованию нелинейных систем автоматического управления.
Пример учета нелинейности привода управляющего органа. Такой пример применительно к системе
самолета с курсовым автопилотом (в упрощенном
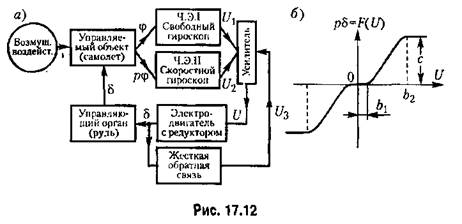
виде) был рассмотрен в работе А. И. Лурье и В. Н. Постникова, Схема данной системы представлена на рис. 17.12, а.
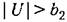 Наклон характеристики и ее криволинейиость могут быт любыми, лишь бы только соблюдались условия Наклон характеристики и ее криволинейиость могут быт любыми, лишь бы только соблюдались условия
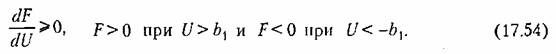
Требуется найти условия устойчивости данной системы.
Уравнение самолета как управляемого объекта в грубо упрощенном виде будет

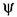 — отклонение курсового угла самолета; 8 — отклонение руля. — отклонение курсового угла самолета; 8 — отклонение руля.
Уравнения чувствительных элементов (гироскопов с потенциометрами):

где F(U) задается графиком рис. 17,12,6.
Уравнения (17.56), (17.57), и (17.58) можно свести к одному:

и безразмерное время

С введением этих переменных дифференциальные уравнения всей системы (17.55). (17.59), (17.60) преобразуются к виду (17.45), а именно:

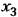 согласно третьему из равенств (17.61). согласно третьему из равенств (17.61).
Установившийся процесс полета при данной системе согласно (17.55), 07.59), (17.60) и графику рис. 17.12, Сбудет иметь место при
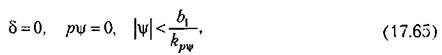
т. е. наличие зоны застоя двигателя приводит к тому, что в установившемся процессе курсовой угол может принять любое постоянное значение в пределах (17.65).
В новых переменных (17.61) установившийся
процесс полета определяется значениями:
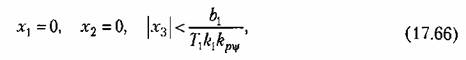
 . Возьмем функцию Ляпунова в виде . Возьмем функцию Ляпунова в виде
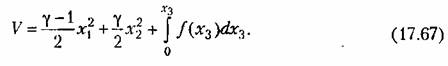
 нечетная (см. нечетная (см.
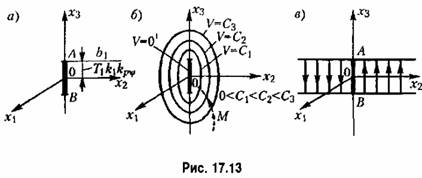
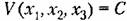 окружают этот отрезок (рис. 17.13, б), стягиваясь к нему с уменьшением С окружают этот отрезок (рис. 17.13, б), стягиваясь к нему с уменьшением С
Составим производную от функции Ляпунова:
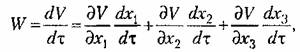
причем частные производные возьмем из (17.67), а производные по безразмерному времени — из уравнений системы (17.63). Тогда
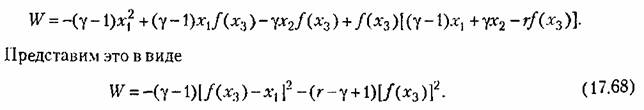
 (рис. 17.13, в). Но вне этой полосы согласно (17.68) она будет всюду отрицательной при (рис. 17.13, в). Но вне этой полосы согласно (17.68) она будет всюду отрицательной при

Поэтому согласно теореме Ляпунова об устойчивости выражение (17.69) является достаточным условием устойчивости рассматриваемой нелинейной системы самолета с курсовым автопилотом (при любой кривизне и любом наклоне характеристики двигателя, имеющей вид рис. 17.12, б).
Траектория изображающей точки М будет пересекать поверхности V= С извне
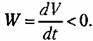 Нужно только проверить, не застрянет ли изображающая точка М там, где W обращается в нуль (помимо отрезка установившегося процесса АВ). В данном случае речь идет о том, не останется ли изображающая точка на полосе (показанной на рис. 17.13, б), где W= 0, если она случайно на нее попадет. Нужно только проверить, не застрянет ли изображающая точка М там, где W обращается в нуль (помимо отрезка установившегося процесса АВ). В данном случае речь идет о том, не останется ли изображающая точка на полосе (показанной на рис. 17.13, б), где W= 0, если она случайно на нее попадет.
Для решения этого вопроса найдем проекции скорости изображающей точки
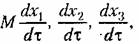 когда эта точка находится в любом месте указанной полосы. Поскольку там когда эта точка находится в любом месте указанной полосы. Поскольку там
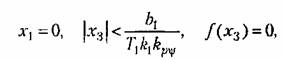
то искомые проекции скорости согласно (17,63) будут
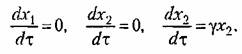
 , с постоянной скоростью, равной ух2 как показано стрелками на рис. 17.13, в. Пройдя полосу изображающая точка снова будет пересекать поверхности V=С извне внутрь, т. е. данная система управления будет устойчивой. , с постоянной скоростью, равной ух2 как показано стрелками на рис. 17.13, в. Пройдя полосу изображающая точка снова будет пересекать поверхности V=С извне внутрь, т. е. данная система управления будет устойчивой.
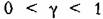 .Для этого случая возьмем функцию Ляпунова в виде .Для этого случая возьмем функцию Ляпунова в виде
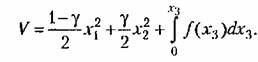
Производная от нее будет
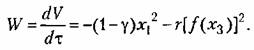
Отсюда аналогично предыдущему приходим к достаточному условию устойчивости системы в виде

 через параметры системы (17.64) принимают вид соответственно через параметры системы (17.64) принимают вид соответственно
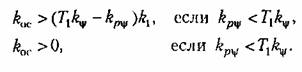
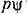 введена в алгоритм управления педс/статочно интенсивно. Из второго же условия устойчивости следует, что система будет устойчива при любой обратной связи, если передаточное число по производной достаточно велико. введена в алгоритм управления педс/статочно интенсивно. Из второго же условия устойчивости следует, что система будет устойчива при любой обратной связи, если передаточное число по производной достаточно велико.
Как видим, данные условия устойчивости не зависят от формы характеристики двигателя (рис. 17.12, б) т. е. они одинаковы при любой кривизне, любом наклоне и любой зоне застоя (в том числе и при однозначной релейной характеристике двигателя постоянной скорости, а также и при линейной характеристике). Такие условия называются условиями абсолютной устойчивости. Они гарантируют, что при их выполнении система будет наверняка устойчива при любой нелинейности с ограничением лишь (17.54). В действительности же система может быть устойчивой и в некоторой области за пределами этих условий устойчивости при конкретно заданной форме нелинейности.
|