Теория систем автоматического управленияЧастотный метод В. М. Попова
Решение задачи об абсолютной устойчивости системы с одной однозначной нелинейностью (т. е. устойчивости при любой форме этой нелинейности со слабым ограничением тина (17,54) или типа рис, 17,14) с помощью теорем прямого метода Ляпунова было проиллюстрировано на двух примерах в § 17.2.
Изложим теперь частотный метод, предложенный румынским ученым В. М. Поповым [69], при использовании которого та же задача решается более просто приемами, аналогичными частотным способам исследования устойчивости линейных систем.
Если в системе автоматического управления имеется лишь одна однозначная нелинейность

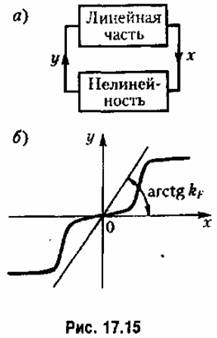
то, объединив вместе все остальные (линейные) уравнения системы, можно всегда получить общее уравнение линейной части системы (рис. 17.15, а) в виде
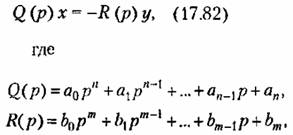

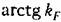 (рис. 17.15, б), т. е. при любом х (рис. 17.15, б), т. е. при любом х

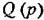 или, что то же, характеристическое уравнение линейной или, что то же, характеристическое уравнение линейной
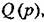 е. не е. не
более двух нулевых полюсов в передаточной функции линейной части системы
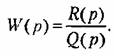
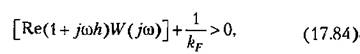
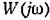 — амплитудно-фазовая частотная характеристика линейной части системы. — амплитудно-фазовая частотная характеристика линейной части системы.
При наличии одного пулевого полюса требуется еще, чтобы
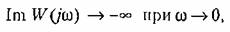
а при двух нулевых полюсах
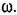
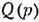 передаточной функции линейной части не более двух чисто мнимых корней, по при этом требуются некоторые другие простые добавочные условия [2], называемые условиями предельной устойчивости. передаточной функции линейной части не более двух чисто мнимых корней, по при этом требуются некоторые другие простые добавочные условия [2], называемые условиями предельной устойчивости.
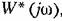 , которая определяется следующим образом: , которая определяется следующим образом:
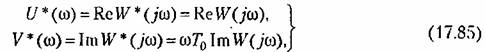
 — нормирующий множитель, — нормирующий множитель,
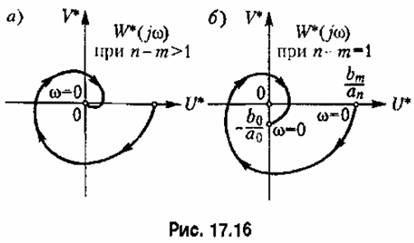
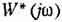 будет на мнимой оси ниже начала координат (рис. 17.16, 6). будет на мнимой оси ниже начала координат (рис. 17.16, 6).
Преобразуем левую часть неравенства (17.84):
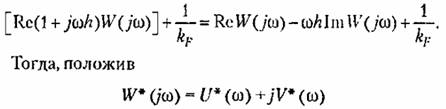
и использовав соотношения (17.85), получим вместо (17.84) для теоремы В. М. Попова условие
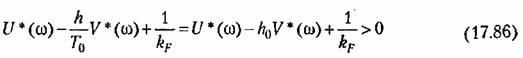
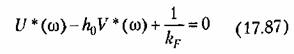 Попова:устойчивости для установления Попова:устойчивости для установления
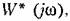 проходящую через точку проходящую через точку
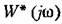 лежала справа от этой прямой. лежала справа от этой прямой.
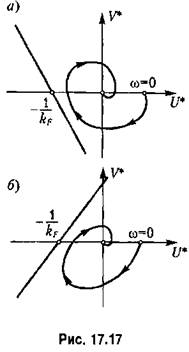
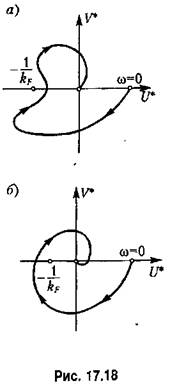
На рис. 17,17 показаны случаи выполнения теоремы. В этих случаях нелинейная система устойчива при любой форме однозначной нелинейности, ограниченной лишь условием (17,83). На рис. 17.18 показаны случаи, когда теорема не выполнятся, т, е, нелинейная система не имеет абсолютной устойчивости.
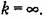 В теореме В.М. Попова при этом вместо (17.84) получаем условие В теореме В.М. Попова при этом вместо (17.84) получаем условие
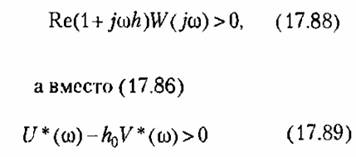
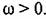 Поэтому в графической интерпретации прямая должна проходить не так, как показано на рис. 17.17, а через начало координат. Поэтому в графической интерпретации прямая должна проходить не так, как показано на рис. 17.17, а через начало координат.
В частности, для указанного примера (§ 17.2) уравнения (17.63) можно преобразовать к виду
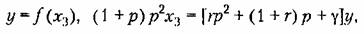
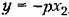 , причем — производная по т. , причем — производная по т.
Передаточная функция линейной части системы будет
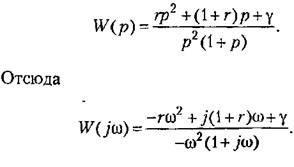
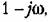 получим получим

Очевидно, что это неравенство может быть выполнено при любом ш > О, если

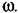
Полученное условие (17.92) выполняется при
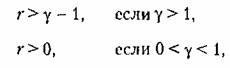
что точно совпадает с найденными ранее условиями абсолютной устойчивости данной системы (17.69) и (17.70). Смысл практической реализации этих условий был раз7>яс-ненв§17.2.
Графически критерий устойчивости выражается в том, что вся кривая
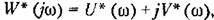 построенная согласно (17.90), расположена (рис. 17.19, а) построенная согласно (17.90), расположена (рис. 17.19, а)
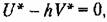
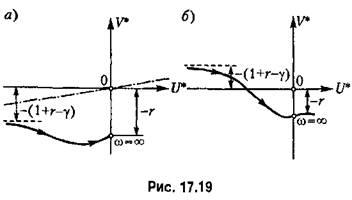
обозначенной штрих пунктиром, со сколь угодно малым наклоном, если
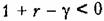 (рис. 17.19, б), то такую прямую провести невозможно и, следовательно, нелинейная система не будет абсолютно устойчивой. (рис. 17.19, б), то такую прямую провести невозможно и, следовательно, нелинейная система не будет абсолютно устойчивой.
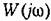 надо перестроить надо перестроить
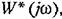 пользуясь формулами (17.85). пользуясь формулами (17.85).
Очертание нелинейности может быть неизвестным. Необходимо лишь знать, в пределах какого угла (рис. 17.15) она расположена. Для конкретно заданных форм нелинейности область устойчивости, вообще говоря, будет несколько шире, но данным методом это не определяется.
|