Теория систем автоматического управленияИсследование систем с переменной структурой
Понятие о системах с переменной структурой было дано в главе 2, а об их уравнениях — в конце главы 16.
Покажем методику исследования систем с переменной структурой при отсутствии внешнего воздействия на примере системы второго порядка при линейном объекте и линейных структурах управляющего устройства, так что нелинейность системы будет заключаться в автоматическом переключении этих структур.
Имея в виду второй порядок системы, используем изображение процессов на фазовой, плоскости, которое для линейных систем представлено было выше на рис. 16.8 -16.13.
 то уравнение системы будет то уравнение системы будет

и получатся незатухающие колебания, изображаемые на фазовой плоскости концентрическими эллипсами (рис. 16.8).
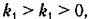 получим уравнения системы получим уравнения системы
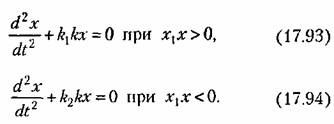

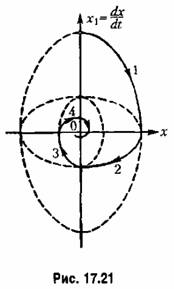
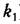 ), далее на эллипс 4, концентрический с эллипсом 2, и т. д. В результате таких переключений система становится устойчивой. ), далее на эллипс 4, концентрический с эллипсом 2, и т. д. В результате таких переключений система становится устойчивой.
В данном примере переходный процесс представляет собой затухающие колебания. В большинстве случаев для избежания колебательных процессов в системах с переменной структурой следует стремиться реализовать скользящий режим. Для этого переключения в системе должны производиться в таких местах, где фазовые траектории направлены навстречу друг другу.
Покажем это на примере. Пусть в тон же системе (рис. 17.20) звено также устроено по принципу рис. 16.27, но



получает другой смысл. Возьмем при этом
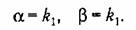
Получим два уравнения системы:

Линиями раздела между областями их действия будут

т. е, ось ординат и наклонная прямая па фазовой плоскости (рис. 17.22). При этом уравнение (17.96) будет действовать в первом и третьем секторах фазовой плоскости.

Поэтому там фазовыми траекториями будут служить согласно рис. 16.8 концентрические эллипсы. Уравнение же (17.97) будет действовать во втором и четвертом секторах фазовой плоскости (рис. 17.22), где фазовые траектории изобразятся в соответствии с рис. 16.3.
Обе эти линейные структуры (17.96) и (17.97) но отдельности не обладают устойчивостью. Благодаря же переключениям система в целом становится устойчивой.
В отличие от предыдущей системы, здесь, как видно из рис. 17.22, нет колебательного процесса. При любых начальных условиях фазовая траектория приходит на наклонную прямую л:, = 0, где она встречается с фазовой траекторией с противоположным ей направлением движения. Поэтому переход изображающей точки через прямую хх = О невозможен. В результате изображающая точка вынуждена двигаться вдоль прямой х{ = О в сторону начала координат, что и представляет собой скользящий режим переходного процесса в дайной системе.
Практически скользящее движение будет сопровождаться вибрациями вследствие быстрых переключений то в одну, то в другую сторону, как и показано на рис, 17.22. Ввиду неидеальности системы (дополнительной инерционности или запаздывания) эти вибрации будут иметь конечные амплитуду и частоту. При идеальном же рассмотрении, проведенном выше, амплитуда их равна пулю, а частота — бесконечности.
Рассмотрение реального переходного процесса скользящего типа с конечными вибрациями за счет дополнительной инерционности, повышающей порядок уравнения, возможно с помощью приближенного метода гармонической линеаризации. Это можно сдедать аналогично рассмотрению медленно меняющихся сигналов в автоколебательных системах (§ 19.2), если за медленно меняющийся сигнал принять основное апериодическое движение в скользящем процессе, а наложенные на него вибрации рассчитать, как автоколебательную составляющую процесса (см. [73]).
|