Теория систем автоматического управленияЧастотный метод определения автоколебаний
 , так как в других случаях получаются более сложные графические построения. , так как в других случаях получаются более сложные графические построения.

а линейной части системы —

Замыкание системы соответствует замене

Подадим на вход нелинейного звена (рис. 18.38, а) синусоидальные колебания

На выходе нелинейного звена получим согласно (18.205) вынужденные колебания

которые можно найти, например, как показано на рис. 18,38, б или в, .
 можно воспользоваться частотным аппаратом, который применялся ранее для линейных систем следующим образом. можно воспользоваться частотным аппаратом, который применялся ранее для линейных систем следующим образом.
Согласно формулам (18.9) приближенная передаточная функция нелинейного звена

 будет будет
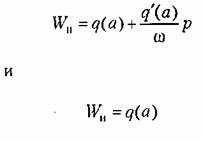
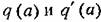 определяются формулами (18.10). определяются формулами (18.10).
 при наличии гистерезисной петли, следовательно, будет при наличии гистерезисной петли, следовательно, будет

а без гистерезисной петли —

Эта характеристика определяет амплитуду и фазу первой гармоники на выходе нелинейного звена (если на его вход подается синусоида), а именно выражение (18.210) можно представить в виде

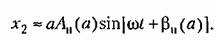
Например, выходная величина х2 релейного звена с характеристикой рис. 18.1, а меняется в процессе вынужденных колебаний по закону, изображенному сплошной ломаной линией на рис. 18.38, в. Пунктиром показана основная синусоида для нее, причем из (18.212) и (18.15) имеем:
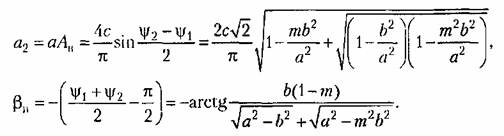
Действительная ступенчатая кривая заменяется в данном случае синусоидой (первая гармоника), вершина которой совпадает с осью симметрии действительного прямоугольника (рис. 18.38, в).
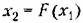 без гистерезисной петли, без гистерезисной петли,
 т. е. т. е.
вынужденные колебания па выходе не имеют фазового сдвига.
 Для более сложных нелинейных звеньев в амплитудно-фазовую характеристику войдет также и частота со. Кроме того, как увидим ниже, зависимость от частоты будет всегда вводиться линейной частью системы. Для более сложных нелинейных звеньев в амплитудно-фазовую характеристику войдет также и частота со. Кроме того, как увидим ниже, зависимость от частоты будет всегда вводиться линейной частью системы.
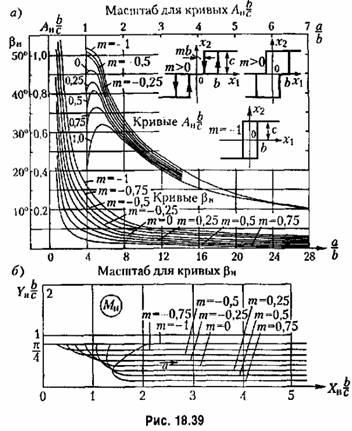
 для наиболее типичных релейных и других простейших нелинейных звеньев. На основании этого строятся приближенные амплитудные и фазовые характеристики путем вычислений по формулам (18.212). Результаты для простейших случаев приведены на рис. 18.39 и 18.40. Там приведены также и обратные амплитудно-фазовые характеристики для наиболее типичных релейных и других простейших нелинейных звеньев. На основании этого строятся приближенные амплитудные и фазовые характеристики путем вычислений по формулам (18.212). Результаты для простейших случаев приведены на рис. 18.39 и 18.40. Там приведены также и обратные амплитудно-фазовые характеристики

На графиках указаны все необходимые обозначения и типы нелинейных характеристик звеньев. Аналогичным путем можно построить графики и для других конкретных нелинейных звеньев.

Общая приближенная амплитудно-фазовая характеристика всей разомкнутой системы с нелинейным звеном будет
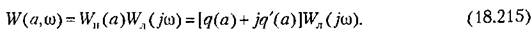

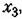 определяемые формулами определяемые формулами

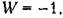 Это и будет в Это и будет в
данном случае условием существования периодического решения для замкнутой нелинейной системы, которое принимается приближенно синусоидальным. Итак, имеем условие

 в случае отсутствия гистерезиспой петли (правая часть (18.218) в этом в случае отсутствия гистерезиспой петли (правая часть (18.218) в этом
случае будет вещественной).
Левая часть уравнения (18.218) или (18.217) представляет собой амплитудно-фазовую характеристику линейной части системы, а правая — обратную амплитудно-фазовую характеристику нелинейного звена (для первой гармоники), взятую с обратным знаком. Решение этого уравнения можно получить графически как точку пересечения

 вещественна, получаем график рис. 18.41,6. вещественна, получаем график рис. 18.41,6.
Вместо (18.217) можно пользоваться также выражением

т. е. искать решение как точку пересечения амплитудно-фазовой характеристики нелинейного звена с обратной амплитудно-фазовой характеристикой линейной части системы, взятой с обратным знаком (рис. 18.41, в и г).
 не чертится в рассмотренном не чертится в рассмотренном

способе. Поэтому высказанное положение надо перенести на свойства кривых



 при разных значениях этих параметров. при разных значениях этих параметров.
Рассмотрим примеры.
|