Передаточные функции систем автоматического управления

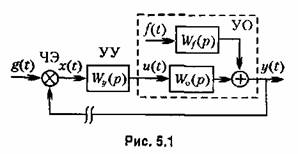
Записанные выше дифференциальные уравнения системы автоматического управления (5.4) и (5.6) могут быть получены также на основании понятия передаточной функции, которое было введено в главе 3. Рассмотрим рис. 5.1, где изображена замкнутая система автоматического управления.

Предположим вначале, что чувствительный элемент (ЧЭ) отсоединен от управляемого объекта (УО), и рассмотрим так называемую разомкнутую систему автоматического управления.

Управляющее воздействие, которое прикладывается к управляемому объекту, определяется выражением

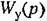— передаточная функция управляющего устройства, которая определяется из дифференциального уравнения управляющего устройства (5.2):

Управляемая величина может быть найдена из выражения

—

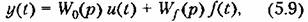
передаточная функция объекта по

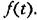
Первая из них определяется из дифференциального уравнения объекта (5.1) при

Передаточную функцию разомкнутой системы можно определить как отношение изображений управляемой величины и ошибки при нулевых начальных значениях и возмущающих воздействиях, равных нулю:

— комплексная величина.

в разомкнутой системе:

— оператор дифференцирования.

Учитывая (5.13), формулу (5.15) можно также записать в виде

Передаточная функция разомкнутой системы имеет весьма большое значение в теории автоматического управления, так как многие методы анализа и синтеза основаны на использовании именно этой функции.

Решая (5.12) и (5.17) совместно, получаем для управляемой величины

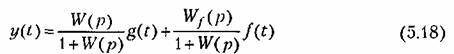
и для ошибки

называется передаточной функцией замкнутой системы. Она устанавливает связь между управляемой величиной и задающим воздействием при равенстве пулю возмущающих воздействий:

называют передаточной функцией замкнутой системы по ошибке. Оно дает связь

между ошибкой и задающим воздействием в замкнутой системе при равенстве нулю возмущающих воздействий:

при нулевых начальных условиях и отсутствии внешних возмущений:

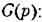
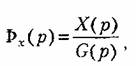
также при пулевых начальных условиях и отсутствии внешних возмущений.

раз по сравнению с отклонением в разомкнутой системе (5.12).

когда цепь управления разорвана и автоматическое управление отсутствует.

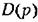представляет собой полином знаменателя передаточной функции замкнутой системы:

  )

Он равен сумме полиномов числителя и знаменателя передаточной функции разомкнутой системы (5.13).

Приравнивание нулю характеристического полинома (5.24) дает характеристическое уравнение замкнутой системы;

Оно может быть записано в более удобной форме, которая непосредственно получается из (5.18) или (5.19):

Полином знаменателя передаточной функции разомкнутой системы С(р) представляет собой характеристический полином разомкнутой системы.

Из рассмотренного видно, что знание передаточной функции разомкнутой системы позволяет найти выражение для ошибки и управляемой величины в функции задающего и возмущающих воздействий, а также характеристическое уравнение системы.

Передаточная функция разомкнутой системы может находиться непосредственно по структурной схеме и передаточным функциям входящих в нее звеньев.