Теория систем автоматического управленияУравнения следящей системы
 . Этот угол должен повторяться на управляемом объекте УО, ось которого является исполнительной осью ИО. Мощность, требуемая Для вращения КО, ничтожна, так как с КО сцеплен только движок потенциометра П]. Мощность, которую может потреблять для своего вращения управляемый объект, . Этот угол должен повторяться на управляемом объекте УО, ось которого является исполнительной осью ИО. Мощность, требуемая Для вращения КО, ничтожна, так как с КО сцеплен только движок потенциометра П]. Мощность, которую может потреблять для своего вращения управляемый объект,


значительно выше и обеспечивается установкой двигателя Л соответствующей поминальной мощности. В этом, а также в дистанционное™ управления заключается смысл использования подобной следящей системы воспроизведения угла поворота.
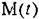 па осп управляемого объекта. па осп управляемого объекта.
Для улучшения динамических качеств следящей системы в ней предусмотрена отрицательная обратная связь но напряжению тахогенератора (ТГ).
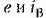 считать также линейной. считать также линейной.
Таким образом, в рассматриваемой системе отпадает необходимость линеаризации и можно сразу приступить к составлению уравнений. Для этой цели разобьем систему на динамические звенья и найдем их передаточные функции.
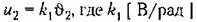 — крутизна, или коэффициент — крутизна, или коэффициент
передачи потенциометра. Напряжение на выходе чувствительного элемента равно разности


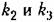 — коэффициенты усиления по напряжению первого и второго усилителей. — коэффициенты усиления по напряжению первого и второго усилителей.
Обмотка возбуждения генератора. Дифференциальное уравнение можно записать на основе второго закона Кирхгофа:

 — суммарные сопротивление и индуктивность цепи возбуждения с учетом — суммарные сопротивление и индуктивность цепи возбуждения с учетом
выходного каскада усилителя.
Приведем это уравнение к стандартному виду:
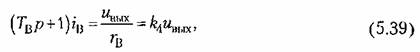
 — постоянная времени цепи возбуждения. — постоянная времени цепи возбуждения.
Отсюда находим передаточную функцию обмотки возбуждения:

Генератор. Для прямолинейной части характеристики намагничивания можно положить

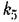 — коэффициент пропорциональности между э. д. с. генератора и током возбуждения в линейной части характеристики. Отсюда получаем передаточную функцию генератора: — коэффициент пропорциональности между э. д. с. генератора и током возбуждения в линейной части характеристики. Отсюда получаем передаточную функцию генератора:

Двигатель. Так как при фиксированном возбуждении двигатель имеет две степени свободы, то необходимо иметь для него два исходных дифференциальных уравнения. Первое уравнение может быть получено, если записать второй закон Кирхгофа для цепи якоря:

Второе уравнение представляет собой закон равновесия моментов на валу двигателя:

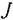 — приведенный коси — приведенный коси
 — угловая скорость двигателя, Ф — поток возбуждения, М — момент нагрузки, приведенный к валу двигателя. — угловая скорость двигателя, Ф — поток возбуждения, М — момент нагрузки, приведенный к валу двигателя.
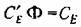
 оператор дифференцирования и решая уравнения (5.43) и (5.44) совместно, получаем оператор дифференцирования и решая уравнения (5.43) и (5.44) совместно, получаем
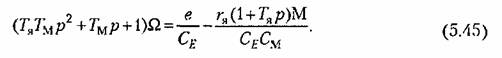
Здесь введены две постоянные времени двигателя; электромеханическая постоянная времени

и постоянная времени якорной цепи

 могут быть найдены из соотношений могут быть найдены из соотношений
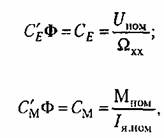
 — номинальные значения напряжения и якорного тока двигателя, — номинальные значения напряжения и якорного тока двигателя,
 — номинальный вращающий момент и скорость идеального холостого хода двигателя. — номинальный вращающий момент и скорость идеального холостого хода двигателя.
Учитывая эти соотношения, электромеханическую постоянную времени можно представить в другом виде:
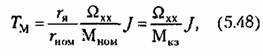
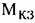 — момент короткого замыкания двигателя (вращающий момент заторможенного двигателя). — момент короткого замыкания двигателя (вращающий момент заторможенного двигателя).
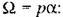
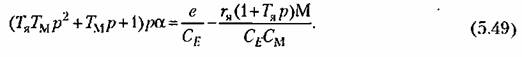
.Из последнего выражения, сравнивая его с формулой (5.12), можно получить передаточную функцию двигателя, связывающую его угол поворота с э. д. с. генератора:
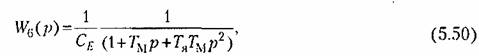
и передаточную функцию по возмущению, связывающую угол поворота а с моментом М, приложенным к его оси:

Редуктор. Считая редуктор линейным безынерционным звеном, запишем его передаточную функцию в виде

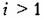 — передаточное отношение редуктора. — передаточное отношение редуктора.
Тахогенератор. Передаточная функция тахогеиератора, в согласии с § 4.7, соответствует идеальному дифференцирующему звену:

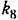 — коэффициент пропорциональности между э. д. с. генератора и скоростью его — коэффициент пропорциональности между э. д. с. генератора и скоростью его
вращения.
Все звенья рассматриваемой системы, кроме тахогеиератора, включены последовательно. Это отображено па структурной схеме рис. 5.10. Тахогенератор включен в цепь местной обратной связи.
Размыкая главную цепь системы, как показано на рис. 5.10 (так, чтобы не нарушать включения местной обратной связи), получаем передаточную функцию разомкнутой системы

После подстановки выражений для передаточных функций звеньев получаем

Здесь введен общий коэффициент усиления цени регулирования без учета действия местной обратной связи

и коэффициент усиления но цени местной обратной связи
 Выражение (5.55) можно переписать в ином виде: Выражение (5.55) можно переписать в ином виде:
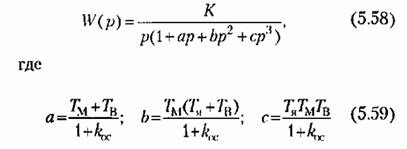
Результирующий коэффициент усиления основной цени с учетом действия местной обратной связи, называемый также добротностью но скорости, будет

Найдем операторные выражения для управляемой величины т32 и ошибки тЗ по общим формулам (5.8) и (5.9). Для этого необходимо найти передаточную функцию по возмущению Му-(р), связывающую угол поворота д2 с возмущением М при разомкнутой главной цепи, но замкнутой цени местной обратной связи. Из структурной
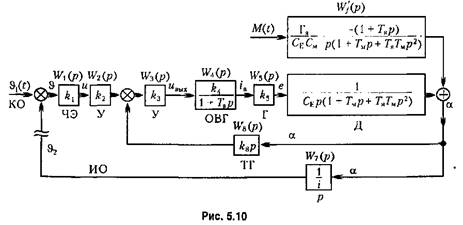
схемы (рис. 5.10) при разомкнутой главной обратной связи и при разомкнутой местной обратной связи
 ) )
где i — передаточное отношение редуктора.
При замыкании местной обратной связи в соответствии с формулой (5.29) получаем

 определяются формулами ( 5.57) и (5.59). определяются формулами ( 5.57) и (5.59).
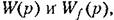 по общим формулам (5.8) и (5.9) находим операторное выражение для управляемой величины по общим формулам (5.8) и (5.9) находим операторное выражение для управляемой величины
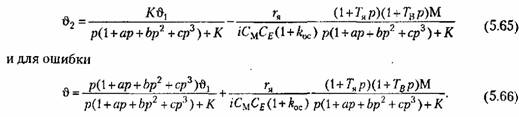

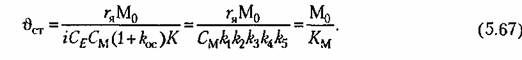
Здесь введено понятие так называемой добротности по моменту (или крутизны по моменту), которая равна отношению приведенного к оси двигателя момента нагрузки к возникающей при этом статической (моментной) ошибке:
 ) )
Из формулы (5.67) видно, что в неподвижном положении ошибка определяется только моментом нагрузки (возмущающим воздействием).
Заметим, что в формулу (5.67) входит момент нагрузки, приведенный к валу двигателя. Поэтому в эту формулу не вошло передаточное отношение редуктора. Если перейти к моменту нагрузки оси управляемого объекта, то в знаменателе последнего выражения (5.67) появится в качестве множителя i. В соответствии с этим можно сформулировать другое понятие добротности по моменту, как отношение момента нагрузки на оси управляемого объекта к установившейся ошибке.
 из из
(5.66) получается установившаяся ошибка
 ) )
Здесь можно ввести понятие добротности по скорости, которая является коэффициентом пропорциональности между скоростью движения следящей системы и возникающей при этом установившейся ошибкой (при отсутствии возмущения). В данном случае она равна общему коэффициенту усиления но разомкнутой цепи
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение

|