Теория систем автоматического управленияУравнения состояния
При решении некоторых задач теории автоматического управления удобнее представлять дифференциальное уравнение объекта (5.1) или дифференциальные уравнения системы (5.4) и (5.6) в виде совокупности дифференциальных уравнений первого порядка. Не умаляя общности, рассмотрим эти уравнения применительно к управляемому объекту.
Пусть объект описывается дифференциальным уравнением n-го порядка (5.1)

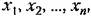 называемых переменными состояния и представим уравнение (5.70) в виде системы дифференциальных уравнений называемых переменными состояния и представим уравнение (5.70) в виде системы дифференциальных уравнений
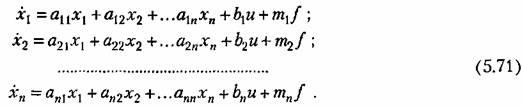
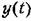 устанавливается алгебраическим уравнением устанавливается алгебраическим уравнением

Обычно уравнения (5.71) и (5.72) записываются в векторпо-матричной форме:

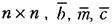 — матрицы-столбцы. Матрицу-столбец- — матрицы-столбцы. Матрицу-столбец-
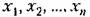 могут иметь неодинаковые размерности. могут иметь неодинаковые размерности.
В выборе переменных состояния имеется определенная свобода. Важно только, чтобы они были независимыми. От того, как выбраны переменные, зависит форма уравнений (5.73) и (5.74), т. е. вид входящих в них матриц.
При нормальной форме уравнений состояния в качестве переменных состояния выбираются сама управляемая величина \п- 1 ее производные:

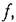 т. с. когда оно имеет вид т. с. когда оно имеет вид

Достоинством нормальной формы является то, что переменные состояния имеют ясный физический смысл, а некоторые из них (например, хих2 и х:]) могут быть непосредственно измерены датчиками различных типов.
Для получения уравнений состояния в канонической форме уравнение объекта (5.70) представляется в виде



Если корни рь Ръ-Рп полинома С0(р) действительные однократные, то правая часть (5.80) может быть представлена в виде суммы элементарных дробей:


где К; и ()г- — коэффициенты разложения.
В качестве неременных состояния выбираются слагаемые суммы (5.81):

Большим достоинством канонической формы является диагоиальиость матрицы Л , что существенно упрощает решение уравнения (5.73). Основной недостаток ее состоит в том, что переменные состояния не имеют ясного физического смысла, в результате чего возникает проблема их непосредственного измерения.
Существуют и другие способы выбора переменных состояния, которые здесь не рассматриваются.
Решение векторно-матричиого уравнения (5.73) может быть представлено в виде
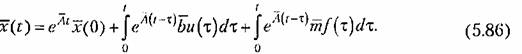
Здесь оно без строгого доказательства построено по аналогии с решением линейного дифференциального уравнения 1-го порядка

общий интеграл которого, как известно, определяется но формуле
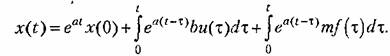
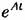 называется переходной или фундаментальной матрицей. Если уравнения состояния представлены в канонической форме, то матрица А диагональная и имеет вид (5.85). Тогда называется переходной или фундаментальной матрицей. Если уравнения состояния представлены в канонической форме, то матрица А диагональная и имеет вид (5.85). Тогда

При других формах уравнений состояния для определения фундаментальной матрицы можно использовать известные способы нахождения матричных функций, например, теоремы Кели—Гамильтона или Сильвестра. Можно также использовать формулу

 — —
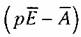
При необходимости можно осуществить обратный переход от уравнений состояния к передаточным функциям объекта. Для этого уравнение (5.73) запишем в изображениях по Лапласу:
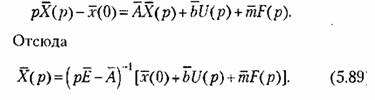
 получается формула (5.88). Из уравнения получается формула (5.88). Из уравнения
(5.74) с учетом (5.89) найдем изображение управляемой величины при нулевых начальных значениях:
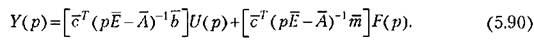
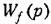
При описании свойств объекта уравнениями состояния возникают две проблемы, нетипичные для случая, когда используется одно дифференциальное уравнение я-то порядка. Эти проблемы рассматриваются в следующем параграфе.
|