Теория систем автоматического управленияПостроение кривой переходного процесса в системах автоматического управления
Общие соображения
Дифференциальное уравнение обыкновенной линейной системы автоматического управления, записанное для ошибки управления, согласно (5.6) имеет вид
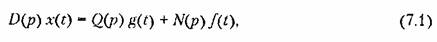
 — возмущающее воздействие. — возмущающее воздействие.
Решение линейного дифференциального уравнения с постоянными коэффициентами (7.1) будет

 вид вид
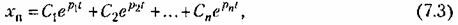

Выражение (7.3) записано для случая отсутствия пулевых и кратных корней.
 определяется правой частью уравне- определяется правой частью уравне-
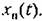
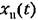

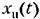 может определяться по отдельности для каждого возмущающего или задающего воздействия независимо от других, а затем их можно складывать, В этом состоит так называемый принцип суперпозиции. может определяться по отдельности для каждого возмущающего или задающего воздействия независимо от других, а затем их можно складывать, В этом состоит так называемый принцип суперпозиции.
Следовательно, если имеется дифференциальное уравнение

то частное решение, определяющее установившийся процесс в системе, будет иметь три слагаемых, каждое из которых определяется частным решением одного из уравнений:

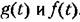
 и стоящих перед ними операторных многочленов оказывает существенное влияние на вид переходного процесса. и стоящих перед ними операторных многочленов оказывает существенное влияние на вид переходного процесса.
При нахождении кривой переходного процесса в системе автоматического управления возникают две трудности. Первая трудность — принципиального характера — заключается в том, что в реальных системах управления управляющие и возмущающие воздействия не являются известными функциями времени, а носят случайный характер. В связи с этим приходится рассматривать некоторые типовые входные воздействия. Типовые входные воздействия стремятся выбирать так, чтобы они были по возможности близкими к реальным воздействиям в системе автоматического управления.
 и систем стабилизации переходный процесс и систем стабилизации переходный процесс
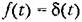 . Эти типовые возмущения изображены на рис. 7.1. . Эти типовые возмущения изображены на рис. 7.1.
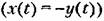 , представляет собой переходную функцию системы для данного возмущения. , представляет собой переходную функцию системы для данного возмущения.
Входная функция второго типа также встречается в системах автоматического управления в виде кратковременного удара нагрузки, например при коротком замыкании электрического генератора, которое прекращается через небольшой промежуток времени системой защиты (плавкие предохранители, максимальные автоматы и
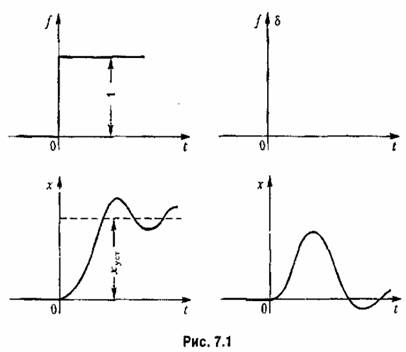
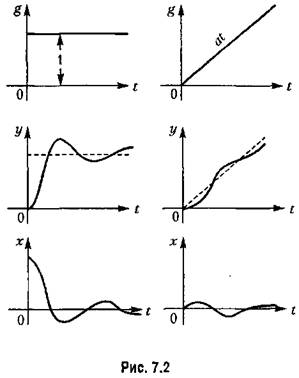
т. п.), при кратковременном возрастании момента нагрузки двигателя и т. д. Реакция системы на воздействие этого типа представляет ее функцию веса.

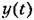 на такое задающее воздействие представляет собой ее переходную функцию для задающего воздействия. на такое задающее воздействие представляет собой ее переходную функцию для задающего воздействия.
Воздействие второго типа является характерным для следящих систем воспроизведения угла, когда командная ось внезапно начинает двигаться с постоянной скоростью.
Возможно изучение поведения системы управления и в том случае, когда входное воздействие представляет собой недетерминированную (определенную), а случайную функцию времени. Этот вопрос будет рассмотрен в главе 11.
Вторая трудность — непринципиального характера — заключается в том, что обычно системы описываются дифференциальными уравнениями сравнительно высокого порядка. Это усложняет практические расчеты; потому для облегчения задачи построения кривой переходного процесса во многих случаях приходится применять вычислительные устройства непрерывного действия и цифровые вычислительные машины.
Для сложных автоматических систем в настоящее время этим методам отдается предпочтение. Важно отметить, что при использовании вычислительных машин часто можно обходиться без составления дифференциальных уравнений тех звеньев автоматической системы, для которых имеются действующие макеты. Тогда для остальной части звеньев набираются их дифференциальные уравнения на вычислительной машине, к которой подключаются имеющиеся действующие макеты. Это свойство можно использовать для испытания и настройки систем в лабораторных условиях.
Ниже будут рассмотрены наиболее распространенные методы построения кривой переходного процесса. К ним относятся метод непосредственного решения линейных дифференциальных уравнений, или так называемый классический метод, использование преобразований Фурье, Лапласа и Карсона-Хевисайда, и использование вычислительных машин.
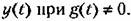
 Непосредственное решение исходного дифференциального уравнения Непосредственное решение исходного дифференциального уравнения
Пусть система автоматического управления описывается линейным дифференциальным уравнением с правой частью

Для отыскания полного решения этого уравнения необходимо найти частное или вынужденное решение уравнения с правой частью хй(1) и определить корни характеристического уравнения
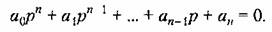
Как указывалось выше, полное решение будет иметь вид


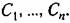
Операции вычисления корней и совместного решения алгебраических уравнений являются трудоемкими. Это особенно относится ко второй операции, так как вычисление корней может быть сделано довольно быстро при помощи стандартных программ для цифровых вычислительных машин. В связи с этим использование этого метода построения кривой переходного процесса ограничивается случаем сравнительно невысокого порядка дифференциального уравнения, обычно не выше третьего.
Расчеты получаются более простыми в том случае, когда правая часть (7.4) равна пулю, т. е. имеется однородное дифференциальное уравнение. Тогда частное решение равно нулю и полное решение (7.5) приобретает более простой вид:
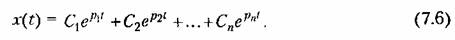
 — начальное значение ускорения. — начальное значение ускорения.
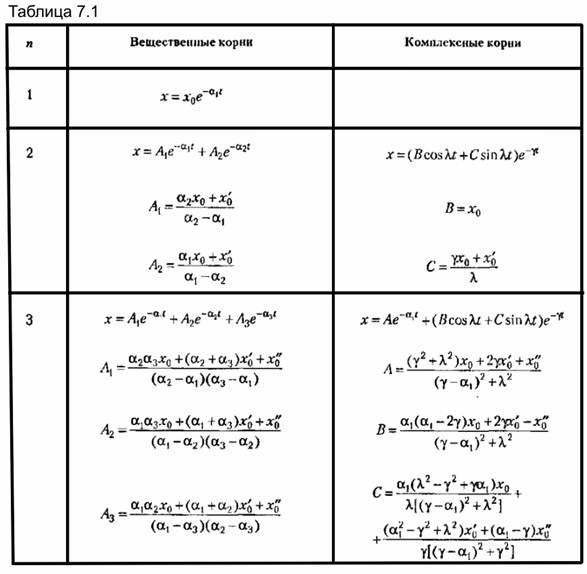
|