Теория систем автоматического управленияСведение неоднородного уравнения к однородному
 , причем еди- , причем еди-


Введем новую переменную
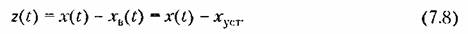
Решение неоднородного уравнения (7,4) для г(С) может быть записано в виде
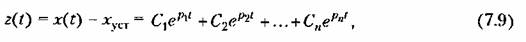
что подобно решению типа (7.6), Этому решению соответствует исходное дифференциальное уравнение без правой части
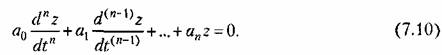
Из уравнения (7.8) нетрудно определить связь между начальными значениями для исходной переменной х и повой переменной г при I = 0:
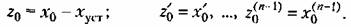
После нахождения решения для переменной г по формуле (7.8) можно легко вернуться к исходной переменной х смещением решения на величину
Однако эти рассуждения пока справедливы для случая, когда степень операторного многочлена в правой части (7.4) равна нулю (?п = 0) и дифференциальное уравнение (7,4) имеет вид

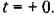 Остановимся па этом вопросе более подробно в случае приложения возмущения тина ступенчатой функции. Остановимся па этом вопросе более подробно в случае приложения возмущения тина ступенчатой функции.
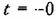 почти всегда принимают нулевые почти всегда принимают нулевые
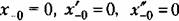 и т, д, В дальнейшем под нулевыми и т, д, В дальнейшем под нулевыми
начальными значениями будем понимать именно эти равенства.
 начальных значений имеют место равенства начальных значений имеют место равенства

Таким образом, для самой координаты и первых (п -т - 1) производных нулевые начальные значения сохраняются и после приложения ступенчатой функции.
Для остальных начальных значений выполняются соотношения

 Если воздействие прикладывается в виде скачка, не равного единице, то вместо следует поставить величину скачка. Если воздействие прикладывается в виде скачка, не равного единице, то вместо следует поставить величину скачка.
П р и м с р. Найдем реакцию системы на единичную ступенчатую функцию при нулевых начальных значениях, т. с. переходную функцию, если дифференциальное уравнение имеет вид

 находим корни: находим корни:

 в соответствии с (7.11) и (7.12), будут в соответствии с (7.11) и (7.12), будут

Определяем установившееся значение искомой координаты:

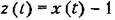 . Начальные значения для новой переменной: . Начальные значения для новой переменной:
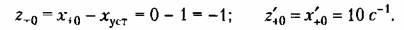
 и случая комплексных корней имеем и случая комплексных корней имеем
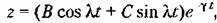
где

Таким образом

Возвращаясь к исходной координате, получаем переходную функцию

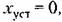 так как в случае так как в случае
 и задача заключается только в отыскании начальных значений при t = +0. и задача заключается только в отыскании начальных значений при t = +0.
 вместо (7.11) для первых п ~ т ~ 2 начальных значений получим вместо (7.11) для первых п ~ т ~ 2 начальных значений получим

и вместо (7.12) для всех остальных начальных значений

 умноженную на время. Если воздействие поступает в виде неединичного импульса, то в эти формулы вместо единицы необходимо подставить заданную величину импульса. умноженную на время. Если воздействие поступает в виде неединичного импульса, то в эти формулы вместо единицы необходимо подставить заданную величину импульса.
 , т. е. перелом кривой, будет уже при т = п - 2, а скачок самой величины х — при т = п - 1. , т. е. перелом кривой, будет уже при т = п - 2, а скачок самой величины х — при т = п - 1.
П р и м е р. Найдем реакцию системы на единичный импульс при нулевых начальных значениях, т. е. функцию веса для дифференциального уравнения, приведенного в предыдущем примере.
Так как в рассматриваемом примере т = п - 1, то в соответствии с (7.14) получим

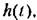
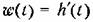
|