Теория систем автоматического управленияЧастотные критерии качества
Под частотными критериями качества будем понимать такие критерии, которые не рассматривают вида переходного процесса, а базируются па некоторых частотных свойствах системы. Частотные критерии качества особенно удобно применять при использовании частотных методов расчета, так как при этом получается наиболее простое решение задачи.
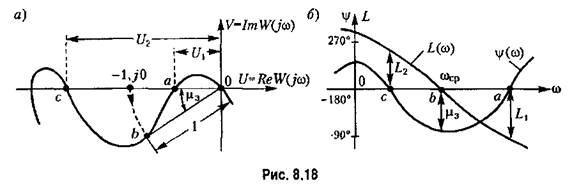
Частотные критерии наиболее разработаны в отношении оценки запаса устойчивости замкнутой системы. Разумеется, что при этом система должна быть устойчивой. Запас устойчивости замкнутой системы можно определять по удалению амплитудно-фазовой характеристики разомкнутой системы (рис. 8.24, а) отточки (-1,;0). Для этой цели вводятся понятия запаса устойчивости по амплитуде (модулю) и запаса устойчивости по фазе.
 выраженными в децибелах: выраженными в децибелах:

Запас устойчивости замкнутой системы по амплитуде равен минимальной из них:

 в линейном масштабе. в линейном масштабе.
 точка Ь может оказаться точка Ь может оказаться
 . Поэтому дополнительно к запасу устойчивости . Поэтому дополнительно к запасу устойчивости


 равному единице (точка Ь на рис. 8.18, а): равному единице (точка Ь на рис. 8.18, а):


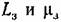 могут быть определены и при использовании логарифмических частотных характеристик разомкнутой системы. могут быть определены и при использовании логарифмических частотных характеристик разомкнутой системы.

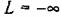 , а фаза , а фаза
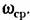
 . В этом отношении более удобно . В этом отношении более удобно
определять запас устойчивости по показателю колебательности. Показателем колебательности называется максимальное значение ординаты Мшах амплитудной характеристики замкнутой системы (см. рис. 8.19) при начальной ординате, равной единице, т. е. относительная высота резонансного пика. Физически эта характеристика

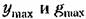 определяется модулем частотной передаточной функции замкнутой системы: определяется модулем частотной передаточной функции замкнутой системы:
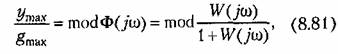
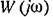 — частотная передаточная функция разомкнутой системы. — частотная передаточная функция разомкнутой системы.
Максимальное значение этого модуля и представляет собой показатель колебательности (имеется в виду наибольший максимум)
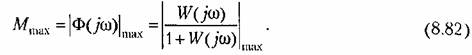
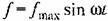 и отыскания относительной величины резонансного пика. и отыскания относительной величины резонансного пика.
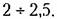
Для отыскания показателя колебательности нет необходимости строить амплитудную частотную характеристику (рис. 8.19) или отыскивать максимум (8.82). Существуют приемы, позволяющие найти показатель колебательности по виду амплитудно-фазовой характеристики разомкнутой системы. Возьмем на амплитудной характеристике (рис. 8.19) некоторую точку а, которой соответствует ордината М, и отобразим эту точку па комплексную плоскость частотной передаточной функции разомкнутой системы. Для этого рассмотрим уравнение

Возводя в квадрат правую и левую части и освобождаясь от знаменателя, после алгебраических преобразований получим
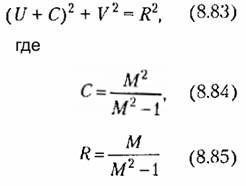 I I
Это есть уравнение окружности с радиусом Я и с центром, смещенным влево от начала координат на величину С.

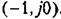
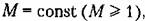 которой коснется амплитудно-фазовая характеристика. которой коснется амплитудно-фазовая характеристика.
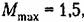 то для выполнения этого необходимо, чтобы амплитудно-фазовая характеристика не заходила в область, ограниченную соответствующей окружностью (рис. 8.21). Лмп-литудно-фазовая характеристика может только коснуться этой окружности. В этом случае показатель колебательности будет как раз равен заданному значению Мтах. то для выполнения этого необходимо, чтобы амплитудно-фазовая характеристика не заходила в область, ограниченную соответствующей окружностью (рис. 8.21). Лмп-литудно-фазовая характеристика может только коснуться этой окружности. В этом случае показатель колебательности будет как раз равен заданному значению Мтах.
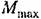 ограничивает ограничивает

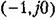 и обеспечивает получение заданного запаса устойчивости, и обеспечивает получение заданного запаса устойчивости,
Величина показателя колебательности может быть определена и в случае использования логарифмических частотных характеристик. Для этого отобразим запретную зону (рис. 8.21) на логарифмическую сетку Рассмотрим отдельно окружность заданного показателя колебательности (рис. 8.22).
На окружности возьмем произвольную точку В и построим вектор, соединяющий эту точку с качалом
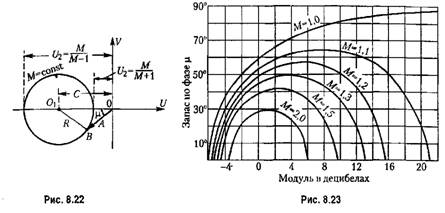
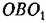 но теореме косинусов находим но теореме косинусов находим

Из рис. 8.22 нетрудно видеть, что зависимость (8.86) существует только для модулей, лежащих в пределах

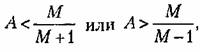 вектора не может попасть в запретную зону (рис. 8.22). вектора не может попасть в запретную зону (рис. 8.22).
 -кривых. Эти графики строятся обычно таким образом, что модуль Л откладывается в децибелах (рис. 8.23). -кривых. Эти графики строятся обычно таким образом, что модуль Л откладывается в децибелах (рис. 8.23).

Из выражения (8.86) можно найти, в частности, максимальный запас по фазе обычным методом отыскания максимума:

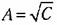 . Если имеется построенная л. а. х. (рис. 8.24), то по имеющимся п.-кривым и при заданном значении М можно достроить требуемое значение запаса по фазе для каждого значения модуля. Это построение должно делаться для модулей, лежащих в пределах (8.87). В результате будет получена запретная область для фазовой характеристики. Чтобы показатель колебательности был не больше заданного значения, фазовая характеристика не должна заходить в эту область. Нетрудно видеть, что определение качественного показателя, характеризующего запас устойчивости, делается здесь одновременно с определением устойчивости. . Если имеется построенная л. а. х. (рис. 8.24), то по имеющимся п.-кривым и при заданном значении М можно достроить требуемое значение запаса по фазе для каждого значения модуля. Это построение должно делаться для модулей, лежащих в пределах (8.87). В результате будет получена запретная область для фазовой характеристики. Чтобы показатель колебательности был не больше заданного значения, фазовая характеристика не должна заходить в эту область. Нетрудно видеть, что определение качественного показателя, характеризующего запас устойчивости, делается здесь одновременно с определением устойчивости.
Удобство показателя колебательности определяется также тем, что запас устойчивости характеризуется здесь одним числом, имеющим для достаточно широкого класса систем сравнительно узкие пределы (1,1-1,5).
 Чем больше h, тем больше ожидаемый запас устойчивости. Чтобы убедиться в этом, рассмотрим два предельных случая. Чем больше h, тем больше ожидаемый запас устойчивости. Чтобы убедиться в этом, рассмотрим два предельных случая.
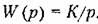 , Тогда замкнутая , Тогда замкнутая
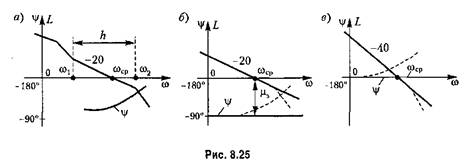
система очень хорошо демпфирована, так как запас устойчивости по амплитуде
 , а показатель колебательности (см. рис. 8.23) М = 1. При наличии дополнительного излома (показано пунктиром на рис. 8.25, б, а также см. рис. 8.24) запас устойчивости уменьшается. , а показатель колебательности (см. рис. 8.23) М = 1. При наличии дополнительного излома (показано пунктиром на рис. 8.25, б, а также см. рис. 8.24) запас устойчивости уменьшается.
 . Нетрудно убедиться, что в этом случае замкнутая система находится на колебательной границе устойчивости, а при наличии дополнительного излома (показано пунктиром) становится неустойчивой. . Нетрудно убедиться, что в этом случае замкнутая система находится на колебательной границе устойчивости, а при наличии дополнительного излома (показано пунктиром) становится неустойчивой.
Таким образом, если л. а. х. разомкнутой системы не имеет асимптоты с наклоном - 20 дБ/дек (или с пулевым наклоном), то не обеспечивается даже устойчивость замкнутой системы.
 будет рассмотрена в §12.6. будет рассмотрена в §12.6.
Оценка быстродействия может производиться по частотным характеристикам замкнутой и разомкнутой системы. При рассмотрении замкнутой системы обычно используется амплитудная частотная характеристика (рис. 8.19).
Для оценки быстродействия по этой характеристике могут использоваться следующие величины:
 — резонансная частота, соответствующая пику а. ч. х.; — резонансная частота, соответствующая пику а. ч. х.;
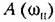 = 0,707; = 0,707;
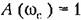 ; ;
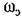 — эквивалентная полоса пропускания замкнутой системы, определяемая но выражению — эквивалентная полоса пропускания замкнутой системы, определяемая но выражению
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение


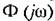
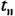 может меняться от долей секунды до нескольких часов и более. может меняться от долей секунды до нескольких часов и более.
 должны устанавливаться для каждой должны устанавливаться для каждой
конкретной системы на основе изучения условий ее эксплуатации. При этом характеризовать быстродействие системы может как вся совокупность указанных выше величин, так и каждая из них в отдельности.
 Эта частота показана, например, на рис. 8.2 и 8,24. Эта частота показана, например, на рис. 8.2 и 8,24.
Определение частоты среза разомкнутой системы может быть сделано па диаграмме, изображенной на рис. 8.18, по точке пересечения а. ф. х. с окружностью единичного радиуса, центр которой расположен в начале координат.
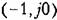

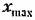
Хотя приведенные выше частотные критерии запаса устойчивости и быстродействия могут рассматриваться независимо от свойств системы во временной области, представляется полезным провести некоторое приближенное сопоставление частотных и временных характеристик.
Если показатель колебательности М > 1, то замкнутую систему можно аппроксимировать колебательным звеном (см. § 4.5). Тогда передаточная функция замкнутой системы может быть представлена в виде

 и показателем колебательности М для той же передаточной функции (8.90). и показателем колебательности М для той же передаточной функции (8.90).
Кривые, приведенные на рис. 8.26, в некоторой мере характеризуют связь между показателями качества и в более сложных случаях, чем выражение
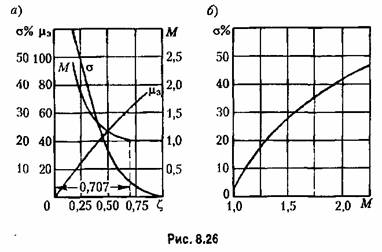
(8.90).
 на переходной характеристике (рис. 8.3) может быть определено по приближенной зависимости на переходной характеристике (рис. 8.3) может быть определено по приближенной зависимости

Если переходный процесс в системе заканчивается за 1-2 колебания, то время переходного процесса можно определить по приближенной зависимости

 и измерять се в Герцах. Тогда получаем и измерять се в Герцах. Тогда получаем

|