Теория систем автоматического управленияСлучайные процессы
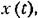 а а
 так же как случайная величина не так же как случайная величина не
имеет определенного значения, а является совокупностью (множеством) возможных значений.
Можно еще сказать, что случайный процесс есть такая функция времени, значение которой в каждый момент времени является случайной величиной.

Примерами случайных процессов могут, например, являться: координаты самолета, замеряемые радиолокационной станцией; угол визирования движущейся цели головкой самонаведения; помехи в системе телеуправления; нагрузка электрической сети и т: и.
 . Каждая кривая множества (рис. 11.11) является лишь отдельной реализацией случайного процесса. Никогда нельзя сказать заранее, по какой кривой пойдет процесс. . Каждая кривая множества (рис. 11.11) является лишь отдельной реализацией случайного процесса. Никогда нельзя сказать заранее, по какой кривой пойдет процесс.
Однако случайный процесс может быть оценен некоторыми вероятностными характеристиками.
 каждая из которых имеет свой закон распределения. Поскольку это — непрерывная случайная величина, то надо пользоваться понятием плотности вероятности. каждая из которых имеет свой закон распределения. Поскольку это — непрерывная случайная величина, то надо пользоваться понятием плотности вероятности.
 будет свой закон распределения; будет свой закон распределения;
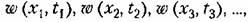
причем по свойству (11.14) для каждого из них

Для каждого заданного момента времени можно найти характеристики случайных величин, определенные в § 11.1. В результате будем иметь сред нее по множеству (математическое ожидание)

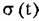 характеризуют рассеяние отдельных возможных реализации процесса около этой средней кривой. характеризуют рассеяние отдельных возможных реализации процесса около этой средней кривой.
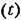 , которое определяется из выражения , которое определяется из выражения

Переход к пределу здесь необходим для того, чтобы характеризовать не какой-нибудь отдельный участок кривой, а всю возможную кривую х (I) в целом.
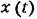 в последующие моменты времени со значениями в предыдущие моменты, вводится понятие двумерной плотности вероятности в последующие моменты времени со значениями в предыдущие моменты, вводится понятие двумерной плотности вероятности
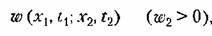
 . Вводится также и -мерная плотность вероятности . Вводится также и -мерная плотность вероятности
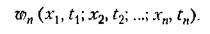
 то это будет вероятность того, что кривая пройдет вблизи заданных п точек. то это будет вероятность того, что кривая пройдет вблизи заданных п точек.
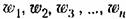 и связью между ними. и связью между ними.
 и т. д. будут независимыми случайными событиями, для которых вероятность их совместного наступления равна, как известно, произведению вероятностей наступления каждого из них в отдельности. Следовательно, для чисто случайного процесса и т. д. будут независимыми случайными событиями, для которых вероятность их совместного наступления равна, как известно, произведению вероятностей наступления каждого из них в отдельности. Следовательно, для чисто случайного процесса
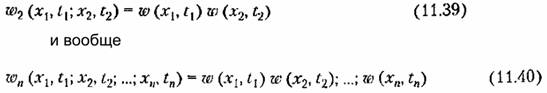
Это — самые простые соотношения в теории случайных процессов. Они могут применяться для характеристики некоторых видов помех (чисто случайные хаотические помехи).
Для характеристики полезных входных сигналов систем управления соотношения (11.39) и (11.40) практически не могут применяться, так как для этих сигналов ход процесса в последующие моменты времени в какой-то степени зависит от того, что было в предыдущие моменты времени.
 не будут независимыми. Чем более инерционен изучаемый объект, тем больше эта взаимозависимость, или корреляция. В таких случаях вместо формулы (11.39) необходимо записать не будут независимыми. Чем более инерционен изучаемый объект, тем больше эта взаимозависимость, или корреляция. В таких случаях вместо формулы (11.39) необходимо записать
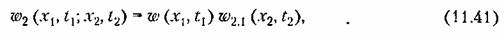
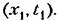
 , можно , можно
найти также и условную плотность вероятности

Кроме того, имеет место следующая связь между основными плотностями вероятности:

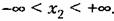
Аналогичным образом любая плотность вероятности низшего порядка всегда может быть получена из высшей, т. е. высшие плотности вероятностей содержат наибольшее количество информации о случайном процессе (о взаимосвязях между возможными значениями случайной величины х в различные моменты времени).

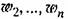 рассматриваются разные типы случайных процессов в отличие от чисто случайных. рассматриваются разные типы случайных процессов в отличие от чисто случайных.
Другая классификация всех случайных процессов состоит в разделении их на стационарные и нестационарные. Теория стационарных случайных процессов наиболее разработана и чаще всего применяется на практике.
|