Теория систем автоматического управленияПрохождение случайного сигнала через линейную систему
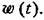 на на

 на основании формулы свертки (7.44) на основании формулы свертки (7.44)

Рассматривая в этой формуле математические ожидания, имеем
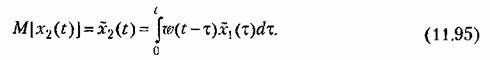
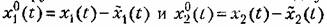 для двух моментов времени; для двух моментов времени;
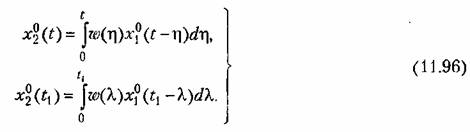
После перемножения получим

Далее, переходя к математическому ожиданию, можно найти корреляционную функцию
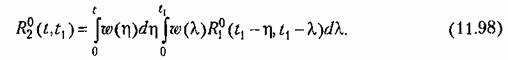
 в формуле (11.98) следует поло- в формуле (11.98) следует поло-
 Тогда Тогда
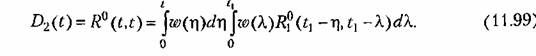
В случае использования канонического разложения случайной функции

выходная величина может быть представлена в виде

 определяется формулой (11.95), а координатные функции определяется формулой (11.95), а координатные функции
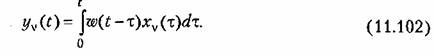
Корреляционная функция выходного сигнала

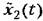 и координатных функций и координатных функций
 в соответствии с выражениями (11.95) и (11.102) могут использоваться различные методы построения переходных процессов (см. главу 7). в соответствии с выражениями (11.95) и (11.102) могут использоваться различные методы построения переходных процессов (см. главу 7).

Однако на выходе линейной системы процесс некоторое время после включения будет устанавливаться и не будет стационарным. Корреляционная функция на выходе может быть получена из общего выражения (11.98):
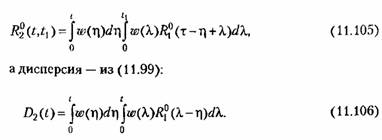
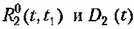 стремятся к не- стремятся к не-
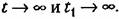


 . Тогда в соответствии с (11.106) дисперсия на выходе будет . Тогда в соответствии с (11.106) дисперсия на выходе будет
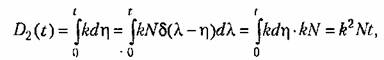
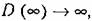
так как звено не является устойчивым, а оно находится на границе устойчивости
(нейтрально-устойчиво).
 выходного сигнала. выходного сигнала.
 соотношением (11.61): соотношением (11.61):

Это же соотношение имеет место и для выходного сигнала:
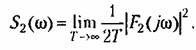
 связаны между собой связаны между собой
посредством частотной передаточной функции:

Отсюда можно найти

Таким образом, спектральная плотность выходной величины может быть получена умножением спектральной плотности входной величины на квадрат модуля частотной передаточной функции линейкой системы. Отметим, что приведенное выше доказательство, вообще говоря, не является строгим, так как существование стационарного случайного процесса на выходе не доказано.
 но преобразованию Фурье (11.66) или (11,68). но преобразованию Фурье (11.66) или (11,68).
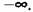
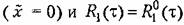 , имеем , имеем
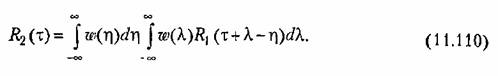
Найдем теперь спектральную плотность для выходного сигнала. Она связана с корреляционной функцией соотношением (11.65):

Подставляя в последнюю формулу значение корреляционной функции из (11.110), получаем
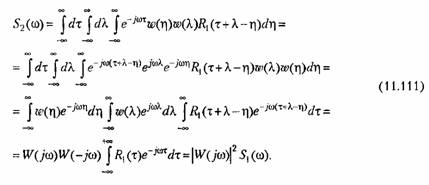
Последнее выражение совпадает с (11.109), что и требовалось доказать. Для нахождения дисперсии, или среднего квадрата выходной величины необходимо проинтегрировать по всем частотам спектральную плотность:

 то на выходе для случайной величины х2 (0 также будет иметь место нормальное распределение. то на выходе для случайной величины х2 (0 также будет иметь место нормальное распределение.
При вычислении интеграла (11.112) обычно приходится иметь дело с подынтегральным выражением вида

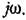
Наивысшую степень знаменателя обозначим 2п. Наивысшая степень числителя в реальной системе может быть на выше 2п — 2. Для удобства интегрирования написанное выше выражение обычно представляют в виде
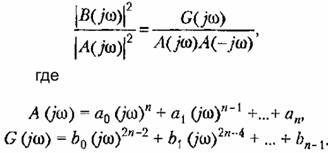
 для устой- для устой-
 означает поворот комплексного числа на угол я/2. означает поворот комплексного числа на угол я/2.

 может быть представлен в виде [ 29 ]: может быть представлен в виде [ 29 ]:

Таким образом, вычисление дисперсии (11.112) можно свести к нахождению интеграла совпадает с точностью до знака со старшим определителем Гурвица, а числитель определяется выражением

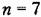 и сведены в таблицы (см. приложение 1). и сведены в таблицы (см. приложение 1).
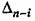 — определитель Гурвица. На колебательной границе устойчивости этот определитель обращается в нуль, а дисперсия выходной величины будет стремиться к бесконечности. — определитель Гурвица. На колебательной границе устойчивости этот определитель обращается в нуль, а дисперсия выходной величины будет стремиться к бесконечности.
В заключение рассмотрим два важных случая прохождения случайного сигнала через линейную систему.
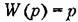 спектральная плотность выходной величины (производной от входной величины) может быть получена умножением спектральной плотности входной величины наш2 спектральная плотность выходной величины (производной от входной величины) может быть получена умножением спектральной плотности входной величины наш2

при двойном дифференцировании — на а/1 и т. д.
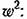

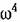 и т. д. и т. д.
|