Теория систем автоматического управленияО синтезе систем с переменными параметрами
Ввиду сложности математического решения синтез систем управления с переменными параметрами, как правило, должен осуществляться при помощи вычислительных машин непрерывного или дискретного действия, а также посредством реального моделирования. Вычислительные машины позволяют просмотреть все наиболее важные режимы работы системы, оценить ее качественные показатели и подобрать необходимые корректирующие средства.
Однако во многих случаях, особенно для квазистационарных систем, можно провести синтез расчетным путем. Это позволяет более сознательно подойти к определению структуры проектируемой системы и параметров корректирующих средств, что значительно сокращает объем последующих исследований и проверок на вычислительных машинах и моделях.
 , что ведет к замораживанию коэффициентов дифференциального уравнения (13.1), В этом случае система с переменными параметрами сводится к системе с постоянными параметрами, что позволяет применять для нее известные методы синтеза (см. главу 12). , что ведет к замораживанию коэффициентов дифференциального уравнения (13.1), В этом случае система с переменными параметрами сводится к системе с постоянными параметрами, что позволяет применять для нее известные методы синтеза (см. главу 12).
 — время работы системы. — время работы системы.
Если во всем рабочем интервале времени от 0 до Ткачество системы управления оказывается приемлемым, то ее считают работоспособной и при изменении коэффициентов уравнения в исследованных пределах.
Этот метод будет давать правильные результаты, если в течение времени переходного процесса (пока функция веса не затухнет практически до нуля) коэффициенты уравнения (13.1) успеют мало изменить свое значение.
Следует заметить, что эффективность рассматриваемого метода может зависеть от правильного выбора фиксированных моментов времени, для которых производится замораживание коэффициентов. Необходимо так выбирать эти моменты времени, чтобы охватить все возможные варианты значений коэффициентов, обратив особое внимание на опасные точки, в которых происходит значительное изменение коэффициента, смена его знака и т. п. Безусловно, что правильный выбор рассматриваемых моментов времени во многом зависит от опыта проектировщика.
 Дифференциальное уравнение ракеты как объекта управления без учета влияния возмущений в простейшем случае может быть представлено в виде [93] Дифференциальное уравнение ракеты как объекта управления без учета влияния возмущений в простейшем случае может быть представлено в виде [93]
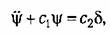
 — угол поворота управляющих органов. — угол поворота управляющих органов.
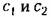 в процессе полета изменяются (рис. 13.5). в процессе полета изменяются (рис. 13.5).
 Заморозим в этих! Заморозим в этих!
точках коэффициенты. Тогда вместо одного уравнения с переменными коэффициентам и получим четыре уравнения с постоянными коэффициентами и, соответственно, четыре стационарных объекта.
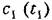 имеет имеет

максимальное отрицательное значение. Передаточная функция объекта для этого случая
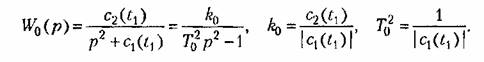
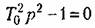 имеется положительный корень, имеется положительный корень,
т. е. объект статически неустойчив. Структурная схема системы угловой стабилизации с таким объектом аналогична изображенной на рис. 6.5. Выберем параметры этой системы исходя из требований точности и запаса устойчивости. При необходимости введем в систему дополнительное корректирующее звено. Желательно, чтобы при тех же значениях параметров обеспечивалось требуемое качество системы с любым из четырех стационарных объектов. В противном случае придется производить коммутацию параметров или даже структуры корректирующих средств в процессе полета ракеты.
|