Теория систем автоматического управленияМетод замороженных реакций
 эквивалентным звеном с постоянными параметрами. Задача оказывается более простой вследствие того, что в большинстве случаев дифференциальное уравнение звена с переменными параметрами может быть сведено к уравнению первого или второго порядка. эквивалентным звеном с постоянными параметрами. Задача оказывается более простой вследствие того, что в большинстве случаев дифференциальное уравнение звена с переменными параметрами может быть сведено к уравнению первого или второго порядка.

Этот метод оказывается более точным, чем метод замороженных коэффициентов, так как при замене звена с переменными параметрами эквивалентным звеном с постоянными параметрами учитывается факт переменности параметров исходного звена, что будет определять вид и параметры эквивалентного звена.
Идея метода заключается в следующем. Пусть имеется некоторая система управления (рис. 13.6), содержащая в своем составе звено с переменными параметрами. Часть системы, соответствующая постоянным параметрам, выделена в отдельное звено.
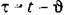 (рис. 13.1), и соответствующая ей (рис. 13.1), и соответствующая ей
передаточная функция


 . Эта весовая функция может быть найдена точно, если дифференциальное уравнение звена имеет первый или второй порядок или приближенными методами в соответствии с изложенным в § 13.2 и § 13.3. Для ее нахождения могут быть также использованы вычислительные машины с последующей аппроксимацией решения. . Эта весовая функция может быть найдена точно, если дифференциальное уравнение звена имеет первый или второй порядок или приближенными методами в соответствии с изложенным в § 13.2 и § 13.3. Для ее нахождения могут быть также использованы вычислительные машины с последующей аппроксимацией решения.
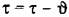 и не зависит от зафиксированного значения смещения. Таким образом, мы получим функцию и не зависит от зафиксированного значения смещения. Таким образом, мы получим функцию
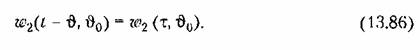
Заметим при этом, что мы фиксируем аргумент г) не полностью, а только в той его части, которая делает рельеф функции веса нецилнндрическим. В результате этого оба разреза (рис. 13.2) получаются одинаковыми, т. е. весовые функции (13.5) и (13.7) совпадают.
Для весовой функции (13.98) может быть найдена передаточная функция



Для системы, изображенной на рис. 13.6, при использовании эквивалентной передаточной функции может быть найдена передаточная функция разомкнутой системы

передаточная функция замкнутой системы
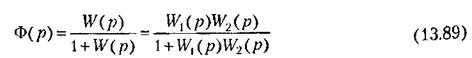
 и передаточная функция но оншоке и передаточная функция но оншоке
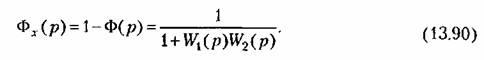
 до Т. до Т.
Как и в случае замороженных коэффициентов, здесь приходится намечать опасные точки, где должно быть проведено исследование. Однако в рассматриваемом методе можно учитывать при этом не только сами значения коэффициентов в отдельные моменты времени, но и характер их изменения во времени (скорость изменения, ускорение изменения и т. д.). Это делает все исследование более полным при сохранении его относительной простоты.
В некоторых случаях оказывается более целесообразным отыскание и последующее замораживание переходной функции звена с переменными параметрами

Для переходной функции (13.18) может быть найдена передаточная функция

По сравнений с нахождением передаточной функции но замороженной весовой функции (13.87) здесь получается обычно более полный учет динамических качеств звена с переменными параметрами. Это оказывается наиболее заметным в тех случаях, когда в правой части дифференциального уравнения звена имеются переменные во времени коэффициенты. Их изменение может быть учтено только при нахождении переходной функции, так как при нахождении весовой функции значения коэффициентов в правой части уравнения фиксируются в момент приложения единичного импульса.
|