Теория систем автоматического управленияЛинейные дискретные системы
ИМПУЛЬСНЫЕ СИСТЕМЫ
Общие сведения
Линейной импульсной системой называется такая система автоматического управления, которая кроме звеньев, описываемых линейными дифференциальными уравнениями, содержит импульсный элемент, преобразующий непрерывное входное воздействие в последовательность импульсов (рис, 14.1, а). Примеры импульсных систем рассмотрены в главе 1.
В общем случае можно изобразить обобщенную структурную схему импульсной системы так, как показано на рис. 14.1,6, где все непрерывные звенья сведены в один блок — непрерывную часть системы 114, Последняя может иметь какую угодно структуру (любой сложности, с обратными связями и т. п.).
Импульсный элемент может представлять собой самостоятельное функциональное устройство (см., например, рис. 1.25) или являться составной частью цифро-аналоговых преобразователей, входящих в систему управления с цифровыми управляющими машинами (ЦВМ). Более подробно системы с ЦВМ будут рассмотрены ниже.
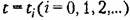 . Чаще всего эти моменты времени равноотстоящие, . Чаще всего эти моменты времени равноотстоящие,
 — период дискретности. В результате импульсной модуляции изменяется какой-либо параметр импульса (амплитуда, ширина). Форма импульсов может быть любой (прямоугольной, трапецеидальной и т.п.), но обычно используются импульсы прямоугольной формы. — период дискретности. В результате импульсной модуляции изменяется какой-либо параметр импульса (амплитуда, ширина). Форма импульсов может быть любой (прямоугольной, трапецеидальной и т.п.), но обычно используются импульсы прямоугольной формы.

Наиболее распространенными в настоящее время видами импульсной модуляции являются амплитудно-импульсная (ЛИМ) и широтио-имиульсная(ШИМ).
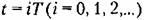 , т. е. значениям: , т. е. значениям:
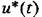 на выходе импульсного элемента на выходе импульсного элемента
 в виде в виде

(рис. 14.2)
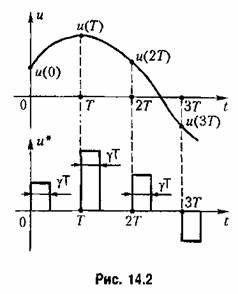
 которая остается постоянной. которая остается постоянной.
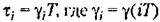 — скважность ?-го импульса. Амплитуда импульсов при этом остается постоянной. Сигнал па выходе импульсного элемента (широтно-импульсиого модулятора) формируется в виде (рис. 14.3) — скважность ?-го импульса. Амплитуда импульсов при этом остается постоянной. Сигнал па выходе импульсного элемента (широтно-импульсиого модулятора) формируется в виде (рис. 14.3)
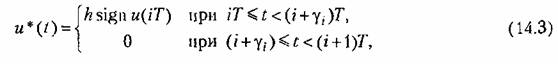
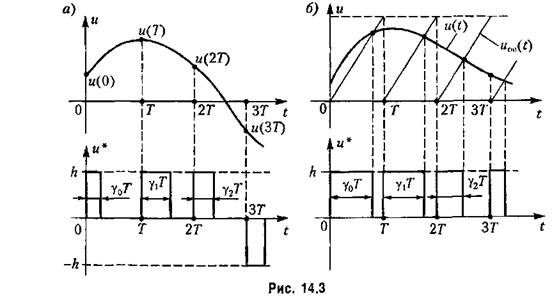
В зависимости от способа определения текущего значения скважности у, различают широтно-импульсную модуляцию 1-го рода (ШИМ-1) и 2-го рода (ШИМ-2). При ШИМ-1 (рис. 14.3, а) скважность /-го импульса
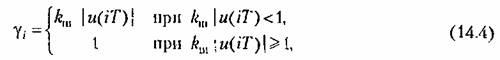
 — коэффициент пропорциональности (крутизна характеристики широтно-импульсного модулятора). — коэффициент пропорциональности (крутизна характеристики широтно-импульсного модулятора).
 е. происходит насыщение модулятора. е. происходит насыщение модулятора.
 не меняет свой знак. Примером может служить система стабилизации напряжения, рассмотренная в главе 1. не меняет свой знак. Примером может служить система стабилизации напряжения, рассмотренная в главе 1.
Широтпо-импульспый модулятор, даже если он в процессе работы системы управления не насыщается, является нелинейным звеном. В этом можно убедиться, восполь-зовавшись принципом суперпозиции, согласно которому реакция линейного звена па сумму входных воздействий должна быть равна сумме реакций.
 I. Пусть I. Пусть
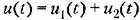 представляет собой ступенчатую фун- представляет собой ступенчатую фун-
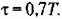
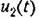 — это последовательность импульсов, — это последовательность импульсов,
 Таким образом, реакция па сумму воздействий не равна сумме реакций и принцип суперпозиции не выполняется. Таким образом, реакция па сумму воздействий не равна сумме реакций и принцип суперпозиции не выполняется.
Рассуждая аналогично, нетрудно убедиться, что амплитудно-импульсный модулятор является линейным звеном. 11оэтому ниже рассматриваются только системы с амплитудно-импульсной модуляцией. Системы управления с широтно-импульспой модуляцией из-за нелинейности самого импульсного элемента (широтно-импульсного модулятора) относятся к нелинейным системам и будут рассмотрены в разделе IV.
|