Теория систем автоматического управленияРазностные уравнения
 модулированных по амплитуде. Несмотря на то, что модулированных по амплитуде. Несмотря на то, что
 Поэтому для исследования импульсных систем вместо дифференциальных уравнений используются так шыъасмые разностные уравнения. Поэтому для исследования импульсных систем вместо дифференциальных уравнений используются так шыъасмые разностные уравнения.
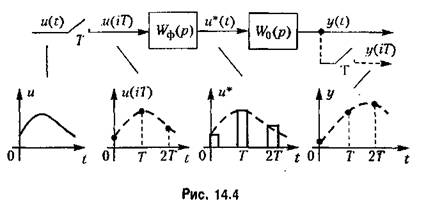
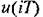 в соответствии с выражением (14.2). Формирующее устройство образует из этих значений импульсы прямоугольной формы так, как показано па рис. 14.2. в соответствии с выражением (14.2). Формирующее устройство образует из этих значений импульсы прямоугольной формы так, как показано па рис. 14.2.
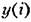 . Условно это отображено на рис. 14.4 наличием ключа па выходе непрерывной части. . Условно это отображено на рис. 14.4 наличием ключа па выходе непрерывной части.
 иногда называют решетчатыми функциями, хотя в строгом понимании они функциями не являются. иногда называют решетчатыми функциями, хотя в строгом понимании они функциями не являются.
 служит конечная разность 1-го порядка или первая разность служит конечная разность 1-го порядка или первая разность

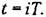

конечная разность 2-го порядка или вторая разность
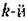 разности можно записать разности можно записать
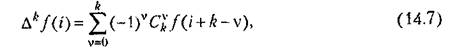
где

— биномиальные коэффициенты.
В качестве аналога дифференциального уравнения можно рассматривать уравнение в конечных разностях. Применительно к системе, изображенной на рис. 14.4, оно имеет вид
 I I

Однако при исследовании дискретных систем удобнее пользоваться уравнением

которое получается из (14.9) с учетом (147). Оно и называется разностным уравнением.
Уравнение (14.10) можно представить и в ином виде:
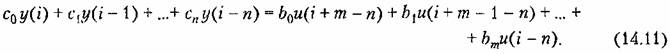

 Такие вычисления легко машинизируются, а также не представляют никаких принципиальных трудностей и при ручном счете (кроме, конечно, затрат времени) даже в случае, когда коэффициенты разностного уравнения с течением времени изменяются. Это отличает разностные уравнения от их непрерывных аналогов — дифференциальных уравнений. Такие вычисления легко машинизируются, а также не представляют никаких принципиальных трудностей и при ручном счете (кроме, конечно, затрат времени) даже в случае, когда коэффициенты разностного уравнения с течением времени изменяются. Это отличает разностные уравнения от их непрерывных аналогов — дифференциальных уравнений.
Общее решение неоднородного разностного уравнения (14.10) или (14.11), как и решение неоднородного дифференциального уравнения, представляется в виде суммы переходной и вынужденной составляющих. Переходная составляющая, т. е. общее решение однородного уравнения, определяется следующим образом:
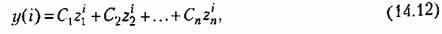
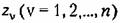 — некратныекорни — некратныекорни

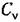 — произвольные постоянные. — произвольные постоянные.
Из (14.12), в частности, вытекает условие затухания свободного движения системы, описываемой разностным уравнением (14.10), т. е. условие устойчивости:
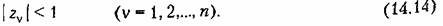
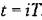 . Во многих случаях этого вполне достаточно для . Во многих случаях этого вполне достаточно для
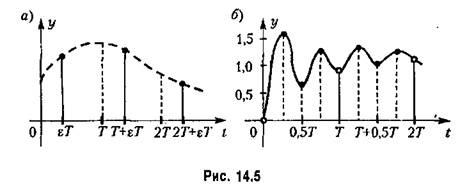
суждения о поведении системы. Если же возникает необходимость в получении информации об изменении выходной величины в любой момент времени, то используется смещенная последовательность (рис. 14.5, а)
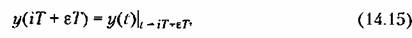
 совпадает с у (с). совпадает с у (с).
Смещенная последовательность у(г, г) представляет собой решение разностного уравнения со смещенным аргументом
 ) )
которое при е = 0 превращается в уравнение (14.10).

Переходная составляющая, т. е. общее решение однородного уравнения, определяется в этом случае следующим образом;
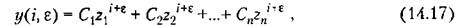
 —некратные корни характеристического уравнения (14.13). —некратные корни характеристического уравнения (14.13).
В качестве примера исследуем процессы в системе, разностное уравнение со смещенным аргументом которой имеет вид

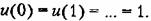
 получим обыкновенное разностное уравнение: получим обыкновенное разностное уравнение:
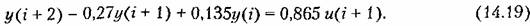
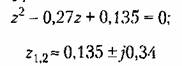 уравнения удоплетворяют условию (14.14). Следовательно, система устойчива. уравнения удоплетворяют условию (14.14). Следовательно, система устойчива.
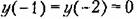 последовательно так за шагом находим значения последовательно так за шагом находим значения
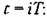
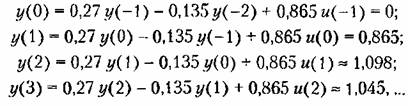
 процесс монотонный, а выходная величина стремится к установившемуся значению процесс монотонный, а выходная величина стремится к установившемуся значению
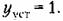
Аналогично решая уравнение(14.18) получим:

 0,75. Таким образом, реальный процесс в системе колебательный затухающий, что не обнаруживается в результате решения уравнения (14.19). 0,75. Таким образом, реальный процесс в системе колебательный затухающий, что не обнаруживается в результате решения уравнения (14.19).
Способы получения разностных уравнений будут рассмотрены в следующих параграфах.
|