Теория систем автоматического управленияПередаточные функции
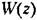 системы, системы,
схема которой представлена на рис. 14.4, легко определяется если известно разностное уравнение (14.10) или (14.11). В соответствии с (14.47) она имеет вид

 — полиномы, входящие в уравнение (14.45). — полиномы, входящие в уравнение (14.45).

Действительно, если известна передаточная функция (14.51), то сразу же определяется уравнение для изображений (14.45). Из него при помощи формул (14,33) или (14.31) получаются разностные уравнения (14.10) или (14.11).
 будем определять непосредственно по структурной схеме системы (рис. 14.4). будем определять непосредственно по структурной схеме системы (рис. 14.4).
 . Тогда, как видно из рис. 14.4, . Тогда, как видно из рис. 14.4,
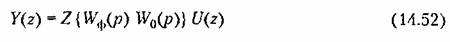
и передаточная функция (14.51) может быть определена следующим образом:

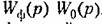 . Это связано с тем что 2-преобразования от произведения передаточных функций непрерывных звеньев, не разделенных импульсным элементом (ключом), не равна произведению z-преобразований: . Это связано с тем что 2-преобразования от произведения передаточных функций непрерывных звеньев, не разделенных импульсным элементом (ключом), не равна произведению z-преобразований:

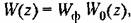 причем причем
 полагается заданной. полагается заданной.
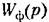 положим, положим,
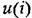
 и и
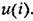
На самом деле никакой импульсный элемент не может генерировать бесконечные по высоте импульсы. Вместе с тем возможность использования указанного формального представления при теоретических исследованиях является обоснованной [49].
 Его изображение в соответствии с (7.7) Его изображение в соответствии с (7.7)
 ) )
Но так как указанная дискрета формально заменяется единичной 8-функцисй, изображение которой по Лапласу (см. табл. 7.2) равно единице, то изображение (14.54) представляет собой передаточную функцию формирующего устройства:
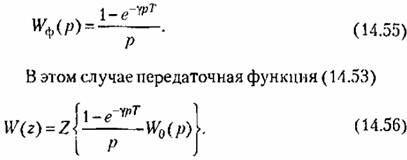
Выражение (14.56) неудобно для практического применения. Поэтому воспользуемся теоремой смещения z-преобразовапия в вещественной области [49], согласно которой

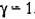 , а само формирующее устройство называется экстраполятором нулевого порядка. Передаточные функции (14.55) и (14.58) при у = 1 принимают вид , а само формирующее устройство называется экстраполятором нулевого порядка. Передаточные функции (14.55) и (14.58) при у = 1 принимают вид
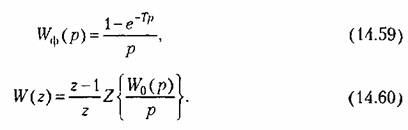
Определим, например, передаточную функцию (14.60) для случая, когда непрерывная часть имеет передаточную функцию
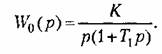
Чтобы можно было использовать данные табл. 14.1, разложим правую часть на простые дроби:

В непрерывную часть системы может входить звено с чистым временным запаздыванием т, что соответствует (см. гл. 6) наличию в передаточной функции Щ)(р) сомножителя е~хр. Если величинах находится в пределах 0<т< 7", то передаточную функцию (14.60) с учетом формулы (14.57) при га^О.^т можно определить следующим образом:
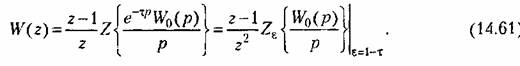 ) )
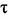 = 0 из (14.61) нельзя получить (14.60), так как при этом е= 1 и смещенная последовательность/^", в) переходит в/(* + 1). Выражения (14.60) и (14,61) совпадут, если последнее в соответствии с формулой (14.33) умножить на г. = 0 из (14.61) нельзя получить (14.60), так как при этом е= 1 и смещенная последовательность/^", в) переходит в/(* + 1). Выражения (14.60) и (14,61) совпадут, если последнее в соответствии с формулой (14.33) умножить на г.
В ряде случаев для получения более полной информации об изменении выходной величины системы применяется так называемая модифицированная передаточная функция
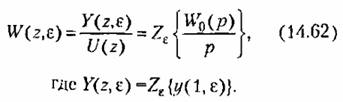

 . Тогда изображение управ- . Тогда изображение управ-


 - передаточная функция разомкнутой системы, которая при использовании - передаточная функция разомкнутой системы, которая при использовании
экстраиолятора нулевого порядка имеет вид (14.60) или (14.61).
 а а
 и из (14.63) получим: и из (14.63) получим:

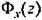 передаточная функция замкнутой системы но ошибке (но своей структуре эти передаточные функции аналогичны передаточным функциям замкнутой непрерывной системы (см. гл.5)). передаточная функция замкнутой системы но ошибке (но своей структуре эти передаточные функции аналогичны передаточным функциям замкнутой непрерывной системы (см. гл.5)).




 представляет собой изображение по представляет собой изображение по

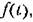 то как отмечалось ранее, то как отмечалось ранее,
При наличии возмущения для разомкнутой системы вместо (14.63) получим

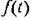 . Однако, как будет показано в § 14.5, это не является препятствием для оценки качества импульсных систем при детерминированных воздействиях. . Однако, как будет показано в § 14.5, это не является препятствием для оценки качества импульсных систем при детерминированных воздействиях.
|