Теория систем автоматического управленияУравнения состояния
Уравнения состояния при непрерывном управлении

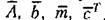
Решение первого из уравнений (14.71), как было показано в главе 5, имеет вид
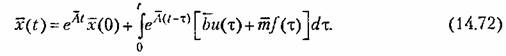
Для дискретных моментов времени из (14.72) получим:
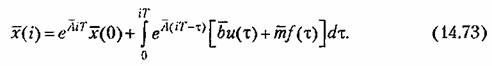
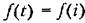 при при
 В реальных системах при малых значениях T это условие, как правило, выполняется. В реальных системах при малых значениях T это условие, как правило, выполняется.
 как это делалось для как это делалось для
разностных уравнений (см. 14.2), получим:

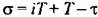
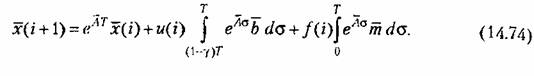
Таким образом, для импульсной системы (рис. 14.4) уравнения состояния можно представить в виде:

 такая же, как и в (14.71). такая же, как и в (14.71).
 . Задача определения этой матрицы может быть решена различными способами [31]. В общем случае предпочтение следует отдать способу, основанному на использовании преобразования Лапласа, согласно которому . Задача определения этой матрицы может быть решена различными способами [31]. В общем случае предпочтение следует отдать способу, основанному на использовании преобразования Лапласа, согласно которому

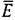 — единичная матрица. — единичная матрица.
 для каждого ее элемента осуществить обратное преобразование Лапласа и в полученных выражениях заменить t на Т. для каждого ее элемента осуществить обратное преобразование Лапласа и в полученных выражениях заменить t на Т.

 вычисляется очень просто: вычисляется очень просто:

Решение первого из уравнений (14.75) можно получить как последовательно шаг за шагом, так и в замкнутой форме. В первом случае вычислительная процедура осуществляется следующим образом:

 и т. д., получим и т. д., получим


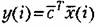 для любого наперед заданного момента времени / = ГГ. для любого наперед заданного момента времени / = ГГ.
Используя уравнения (14.75), можно определить передаточные функции рассматриваемой системы. Для этого найдем z-преобразоваиия от их левых и правых частей с учетом формулы (14.33) при нулевых начальных значениях. В результате получим:
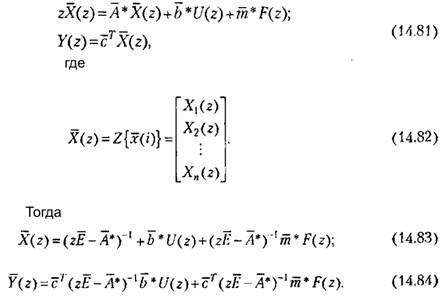
Таким образом, передаточные функции системы определяются следующим образом:

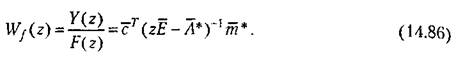

|