Теория систем автоматического управленияУстойчивость импульсных систем
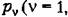
 отображает левую полуплоскость плоскости р в область, ограниченную окружностью единичного радиуса на плоскости г (рис. 14.8, б). При этом мнимая ось плоскости р отображается в саму окружность, отображает левую полуплоскость плоскости р в область, ограниченную окружностью единичного радиуса на плоскости г (рис. 14.8, б). При этом мнимая ось плоскости р отображается в саму окружность,
 Тогда Тогда

 попадают на окружность единичного радиуса плоскости z. попадают на окружность единичного радиуса плоскости z.
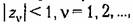 n что совпадает с результатом (14 14). Если хотя бы один корень лежит вне круга единичного радиуса, то система неустойчива. n что совпадает с результатом (14 14). Если хотя бы один корень лежит вне круга единичного радиуса, то система неустойчива.
Окружность единичного радиуса представляет собой границу устойчивости для импульсной системы.
Система находится на апериодической границе устойчивости, если в ее характеристическом уравнении

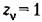 , а остальные корни располагаются внутри круга единичного ради- , а остальные корни располагаются внутри круга единичного ради-

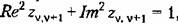 , то имеет место колебательная граница устойчивости. В этом , то имеет место колебательная граница устойчивости. В этом

 может быть положительной, как на рис. 14.8, г, отрицательной или нулевой. может быть положительной, как на рис. 14.8, г, отрицательной или нулевой.
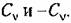
 . Тогда в соответствии с выражениями (14.64) или (14.65) характеристическое уравнение замкнутой системы (14.88) может быть получено следующим образом: . Тогда в соответствии с выражениями (14.64) или (14.65) характеристическое уравнение замкнутой системы (14.88) может быть получено следующим образом:
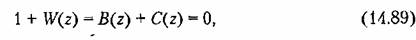

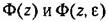 могут иметь различное число корней [30]. Эти случаи здесь не рассматриваются. могут иметь различное число корней [30]. Эти случаи здесь не рассматриваются.
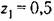 находится внутри круга единичного радиуса. находится внутри круга единичного радиуса.
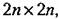 где п — порядок характеристического уравнения. Поэтому на практике этот критерий применяется редко. где п — порядок характеристического уравнения. Поэтому на практике этот критерий применяется редко.
 Однако в результате такой замены уравнение (14.88) Однако в результате такой замены уравнение (14.88)
станет трансцендентным. Вместе с тем в теории функций комплексного переменного существует преобразование

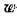 -преобразованием. Оно тоже отображает круг единичного радиуса палевую полуплоскость, но уже не плоскости/?, а плоскости переменной ге>. -преобразованием. Оно тоже отображает круг единичного радиуса палевую полуплоскость, но уже не плоскости/?, а плоскости переменной ге>.
Рассмотрим, например, характеристическое уравнение (14.88) при п = 1. После подстановки (14.90) получим:

Для уравнений первого и второго порядка, как показано в главе 6, необходимое и достаточное условие устойчивости сводится к требованию положительности коэффициентов. Таким образом, условия устойчивости импульсной системы при п = 1 имеют вид

При п ~ 2 характеристическое уравнение и условия устойчивости следующие:

 кроме положительности коэффициентов должно дополнительно выполняться условие критерия Гурвица (см. гл.6). Поэтому для исследования устойчивости требуется проверить выполнение пяти неравенств: кроме положительности коэффициентов должно дополнительно выполняться условие критерия Гурвица (см. гл.6). Поэтому для исследования устойчивости требуется проверить выполнение пяти неравенств:
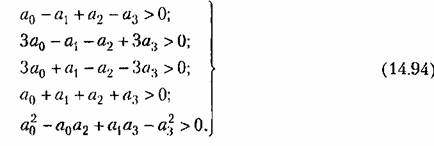 I I
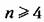 условия устойчивости становятся слишком громоздкими. условия устойчивости становятся слишком громоздкими.
В качестве примера исследуем устойчивость замкнутой системы, передаточная функция непрерывной части которой
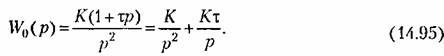
В соответствии с (14.60) при помощи табл. 14.1 находим передаточную функцию
разомкнутой системы:

Характеристическое уравнение замкнутой системы (14.89) имеет вид
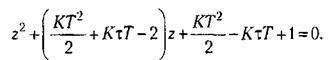
Из неравенств (14.93) получаем условия устойчивости замкнутой системы:

 получим; получим;
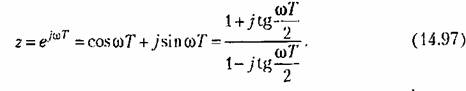
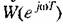 . Определив модуль и фазу или вещественную и мнимую части этой функции, можно построить а. ф. х. разомкнутой системы. . Определив модуль и фазу или вещественную и мнимую части этой функции, можно построить а. ф. х. разомкнутой системы.
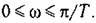
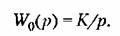
В соответствии с (14.60) находим передаточную функцию разомкнутой системы

В результате замены (14.97) получим
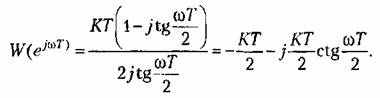
 она она
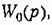 дополняем ее четвертью окружности бесконечно большого радиуса. дополняем ее четвертью окружности бесконечно большого радиуса.
 а. ф. х. заканчивается на критическом отрезке, т. е. имеет место -1/2 перехода. а. ф. х. заканчивается на критическом отрезке, т. е. имеет место -1/2 перехода.
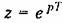 частотная передаточная функция частотная передаточная функция
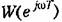 является трансцендентной. Поэтому для систем выше второго порядка построение а. ф. х. существенно затрудняется. Кроме того, практически исключается возможность построения асимптотических логарифмических частотных характеристик. является трансцендентной. Поэтому для систем выше второго порядка построение а. ф. х. существенно затрудняется. Кроме того, практически исключается возможность построения асимптотических логарифмических частотных характеристик.
Для преодоления указанных недостатков удобно использовать преобразование

 что дает возможность применять все критерии устойчивости непрерывных систем. что дает возможность применять все критерии устойчивости непрерывных систем.
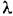 называется абсолютной псевдочастотой, или сокращенно — псевдочастотой. Сравнив (14.99) с (14.97) получим: называется абсолютной псевдочастотой, или сокращенно — псевдочастотой. Сравнив (14.99) с (14.97) получим:

 псевдочастота практически совпадаете реальной частотой (о. псевдочастота практически совпадаете реальной частотой (о.
 при исследовании непрерывных систем. при исследовании непрерывных систем.
В качестве примера используем подстановку (14.99) в передаточной функции (14.97). В результате получим частотную передаточную функцию разомкнутой системы
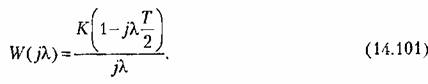
Теперь для исследования устойчивости замкнутой системы можно применять как алгебраический критерий, так и критерий Найквиста.
В первом случае находим характеристическое уравнение замкнутой системы:
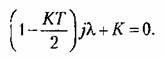
 Для системы первого порядка оно является и достаточным. Для системы первого порядка оно является и достаточным.
Во втором случае находим модуль и фазу:
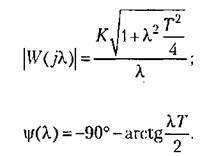
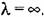

 Па сопрягающей Па сопрягающей
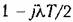
 , а модуль не равен бесконечности. Следовательно, имеет место -1/2 перехода и замкнутая система неустойчива. , а модуль не равен бесконечности. Следовательно, имеет место -1/2 перехода и замкнутая система неустойчива.
|