Теория систем автоматического управленияОценка качества импульсных систем
Общие соображения по оценке качества систем автоматического управления, рассмотренные в § 8.1, относятся и к импульсным системам.
Для оценки точности можно использовать величину ошибки в типовых режимах. В первых трех из них при отсутствии возмущения значение установившейся ошибки в любой момент времени в соответствии с теоремой о конечном значении (14.37) определяется по формуле
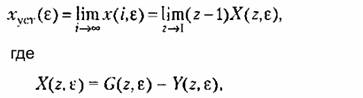
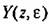 определяется выражением (14.77). определяется выражением (14.77).
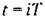

где Х(z) определяется выражением (14.65).
 будет постоянным и импульсная система может рассматриваться как непрерывная. В этом случае для опенки точности, в том числе и возмущающих воздействий, можно пользоваться формулами, приведенными в § 8.2. будет постоянным и импульсная система может рассматриваться как непрерывная. В этом случае для опенки точности, в том числе и возмущающих воздействий, можно пользоваться формулами, приведенными в § 8.2.
Установившаяся точность импульсной системы может оцениваться и по коэффициентам ошибок. Аналогично непрерывным системам, начиная с некоторого момента времени ошибку можно представить в виде ряда
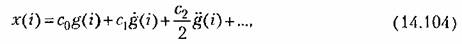
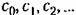 представляют собой коэффициенты разложения представляют собой коэффициенты разложения
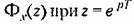 вряд Маклорена по степеням, т. е. вряд Маклорена по степеням, т. е.

Оценка качества импульсной системы может делаться построением кривой переходного процесса, что при использовании г-преобразования осуществляется сравнительно легко.
 Можно Можно
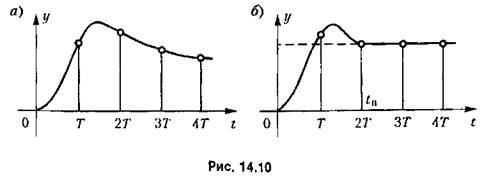
показать, что процессы, подобные изображенному на рис. 14.5, б, будут исключены, если
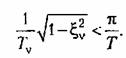
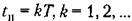 (рис. 14.10, б). Для этого параметры системы должны быть выбраны так, чтобы корни характеристическою уравнения (14.91) располагались в начале координат на плоскости г. Тогда передаточная функция замкнутой системы принимает вид (рис. 14.10, б). Для этого параметры системы должны быть выбраны так, чтобы корни характеристическою уравнения (14.91) располагались в начале координат на плоскости г. Тогда передаточная функция замкнутой системы принимает вид
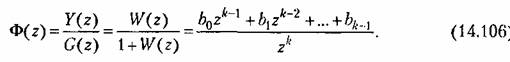 ) )
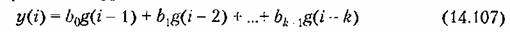 разностное уравнение разностное уравнение
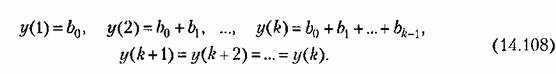
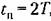 , если , если
Следует однако учитывать, что системы с процессами конечной длительности часто имеют малый запас устойчивости. Так, во втором из рассмотренных случаев при указанных параметрах передаточная функция (14.96) имеет вид
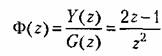
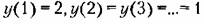
Запас устойчивости по амплитуде и по фазе и показатель колебательности замкнутой системы для импульсных систем определяется точно так же, как и для непрерывных систем (§ 8.8). Отличие состоит только в виде частотных характеристик этих систем.
Рассмотрим, например, систему, передаточная функция которой в разомкнутом состоянии имеет вид (14.96):
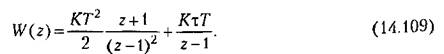
Воспользуемся для расчета методом логарифмических частотных характеристик, С этой целью в (14.109) сделаем подстановку (14.99). В результате получим частотную передаточную функцию разомкнутой системы

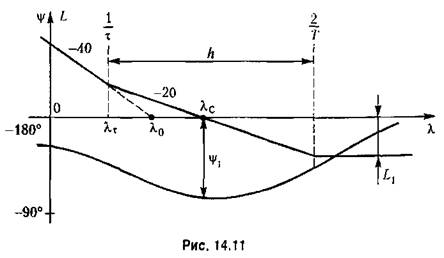
 изображены на рис. 14.11. изображены на рис. 14.11.
Асимптотическая л. а. х. построена в соответствии с выражением (14.110). Ее
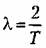
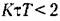
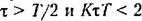 замкнутая система устойчива, так как л. ф. х. не пересекает критический отрезок. Запас устойчивости замкнутой системы но амплитуде (см. §8.8) замкнутая система устойчива, так как л. ф. х. не пересекает критический отрезок. Запас устойчивости замкнутой системы но амплитуде (см. §8.8)

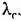 В соответствии со свойствами треугольников на плоскости л. ч. х., гипотенузы которых имеют наклоны -20 дБ/дек и -40 дБ/дек, имеем: В соответствии со свойствами треугольников на плоскости л. ч. х., гипотенузы которых имеют наклоны -20 дБ/дек и -40 дБ/дек, имеем:
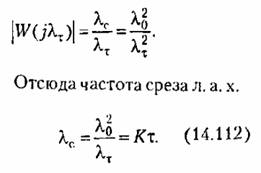
Таким образом, запас устойчивости замкнутой системы по фазе
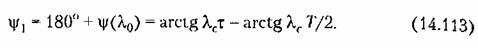
Для определения показателя колебательности замкнутой системы М необходимо при помощи ц-кривых (рис. 8.23) построить запретную область так, как показано на рис. 8.24. При этом параметры Кл и Т должны быть заданы численно. В данном случае можно найти такие значения этих параметров, при которых будет обеспечено наперед заданное значение показателя колебательности.
Нетрудно видеть, что случай (рис. 14.11) по расположению фазовой характеристики сводится к случаю л. а. х. типа 2-1-2, изображенной на рис. 12.10. Используя полученные в главе 12 формулы, получаем оптимальную протяженность участка с наклоном -20 дБ/дек:

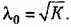 Далее имеем связь между постоянной времени т Далее имеем связь между постоянной времени т
и базовой частотой:
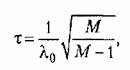
откуда находим коэффициент передачи разомкнутой системы
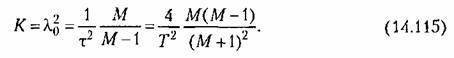
Эту формулу можно записать также в следующем виде:

Формулы (14.115) и (14.116) позволяют выбрать значение коэффициента переда чи непрерывной части системы А* и постоянной времени т при заданном периоде дискретности Гили определить значение периода дискретности при заданном К.
Более детально решение задачи синтеза импульсных систем с заданными показателями качества рассматриваются в главе 15.
|