Теория систем автоматического управленияСлучайные процессы в импульсных системах
 Будем рассматривать стационарные Будем рассматривать стационарные
процессы, когда вероятностные характеристики не зависят от времени.
Среднее значение случайного стационарного процесса

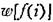 — одномерная плотность вероятности. — одномерная плотность вероятности.
Для центрированных процессов среднее значение равно нулю. Введем понятие корреляционной функции

Аналогично главе 11 можно сформулировать основные свойства корреляционной Функции.
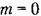
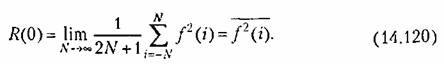
2. При т = 0 корреляционная функция достигает наибольшего значения:

3. Корреляционная функция является четной:

 можно ввести понятие взаимной корреляционной функции можно ввести понятие взаимной корреляционной функции
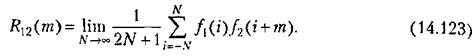
Свойства ее схожи со свойствами взаимной корреляционной функции для непрерывных процессов.
Введем понятие спектральной плотности случайного стационарного процесса как двустороннего 2-преобразования корреляционной функции

 для того, чтобы сделать физическую размерность спектральной плотности дискретного случайного процесса равной размерности спектральной плотности непрерывного процесса и сохранить ее физический смысл. Однако это не обязательно. Аналогично непрерывному случаю можно ввести понятие спектральной плотности как функции круговой частоты для того, чтобы сделать физическую размерность спектральной плотности дискретного случайного процесса равной размерности спектральной плотности непрерывного процесса и сохранить ее физический смысл. Однако это не обязательно. Аналогично непрерывному случаю можно ввести понятие спектральной плотности как функции круговой частоты

 -преобразованию, используя подстановку (14.92), а затем перейти к псевдочастотс посредством -преобразованию, используя подстановку (14.92), а затем перейти к псевдочастотс посредством
 В результате получим В результате получим

Аналогичным образом может быть определена взаимная спектральная плотность двух процессов.
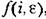 , корреляционная функция , корреляционная функция
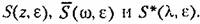
Основное свойство спектральной плотности, как и в непрерывном случае, заключается в том, что интеграл от нее по всем частотам дает средний квадрат случайной величины. Можно показать [96], что в дискретном случае соответствующая формула имеет вид

Выражение (14.129) обычно является более удобным для расчетов по сравнению с (14.128), так как позволяет использовать таблицы интегралов (см. приложение 1).
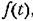 представляющей собой центрированную помеху, эффективное время корреляции представляющей собой центрированную помеху, эффективное время корреляции

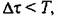 то такой процесс может быть представлен как дискретный белый шум с корреляционной функцией то такой процесс может быть представлен как дискретный белый шум с корреляционной функцией

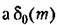 — единичная импульсная функция, равная единице при т*0и равная нулю при т * 0. Этому белому шуму соответствует спектральная плотность — единичная импульсная функция, равная единице при т*0и равная нулю при т * 0. Этому белому шуму соответствует спектральная плотность

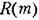
 Спектральная плотность может быть получена использованием формул (14.124)—(14.127). Спектральная плотность может быть получена использованием формул (14.124)—(14.127).
В табл. 14.2 приведены некоторые типовые дискретные стационарные случайные процессы.

 аналогично непрерывному случаю, можно найти спектральную плотность умножением спектральной плотности входного сигнала на квадрат модуля частотной передаточной функции: аналогично непрерывному случаю, можно найти спектральную плотность умножением спектральной плотности входного сигнала на квадрат модуля частотной передаточной функции:

Интегрирование спектральной плотности по всем частотам в соответствии с
 Это Это
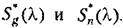 Тогда спектральная плотность ошибки Тогда спектральная плотность ошибки

 — частотные передаточные функции замкнутой системы и замкнутой системы по ошибке. — частотные передаточные функции замкнутой системы и замкнутой системы по ошибке.
Глава 15. Цифровые системы 445
Интегрирование (14 Л 34) по всем частотам в соответствии с (14.129) дает средний квадрат ошибки
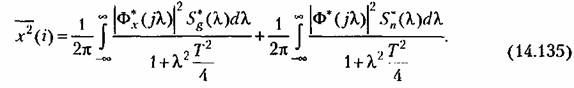
Подобным же образом могут быть найдены расчетные формулы и для других возможных случаев.
|